练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某公司组织员工到附近的景点旅游，根据旅行社提供的收费方案，绘制了如图所示的图象，图中折线ABCD表示人均收费y（元）与参加旅游的人数x（人）之间的函数关系．

    （1）当参加旅游的人数不超过10人时，人均收费为元；
    （2）如果该公司支付给旅行社3600元，那么参加这次旅游的人数是多少？

    【答案】
    （1）240
    （2）解：∵3600÷240=15，3600÷150=24，

    ∴收费标准在BC段，

    设直线BC的解析式为y=kx+b，则有 ，

    解得 ，

    ∴y=﹣6x+300，

    由题意（﹣6x+300）x=3600，

    解得x=20或30（舍弃）

    答：参加这次旅游的人数是20人．


    【解析】（1）观察图象可知：当参加旅游的人数不超过10人时，人均收费为240元，所以答案是240；（2）先判断人数在哪一段，通过计算知,人数介于10到25之间，即BC段，再用待定系数法求解.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

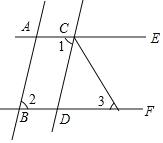
    【题目】如图，已知AB∥CD，∠1=∠2，CF平分∠DCE．

    （1）试判断直线AC与BD有怎样的位置关系？并说明理由；

    （2）若∠1=80°，求∠3的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，把△ABC沿EF对折，叠合后的图形如图所示．若∠A=60°，∠1=90°，则∠2的度数为（ ）

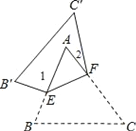
    A. 24°B. 25°C. 30°D. 35°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，BC=2，A为半径为1的⊙B上一点，连接AC，在AC上方作一个正六边形ACDEFG，连接BD，则BD的最大值为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算：
    （1）；
    （2）.
    （1）tan60°﹣|﹣2|+
    （2）（1+ ）÷ ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知：在平行四边形ABCD中，点E，F，G，H分别在边AB，BC，CD，DA上，AE=CG，AH=CF，且EG平分∠HEF．求证：

    （1）△AEH≌△CGF；
    （2）四边形EFGH是菱形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为倡导“低碳生活”，人们常选择以自行车作为代步工具、图（1）所示的是一辆自行车的实物图．图（2）是这辆自行车的部分几何示意图，其中车架档AC与CD的长分别为45cm和60cm，且它们互相垂直，座杆CE的长为20cm．点A、C、E在同一条直线上，且∠CAB=75°．（参考数据：sin75°=0.966，cos75°=0.259，tan75°=3.732）

    （1）求车架档AD的长；
    （2）求车座点E到车架档AB的距离（结果精确到1cm）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，将两个完全相同的三角形纸片ABC和DEC重合放置，其中∠C=900，∠B=∠E=300.

    （1）操作发现如图2，固定△ABC，使△DEC绕点C旋转。当点D恰好落在BC边上时，填空：线段DE与AC的位置关系是 ；

    ② 设△BDC的面积为S1，△AEC的面积为S2。则S1与S2的数量关系是 。

    （2）猜想论证

    当△DEC绕点C旋转到图3所示的位置时，小明猜想（1）中S1与S2的数量关系仍然成立，并尝试分别作出了△BDC和△AEC中BC，CE边上的高，请你证明小明的猜想。

    （3）拓展探究

    已知∠ABC=600，点D是其角平分线上一点，BD=CD=4，OE∥AB交BC于点E（如图4），若在射线BA上存在点F，使S△DCF =S△BDC,请直接写出相应的BF的长

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了促进学生多样化发展，某校组织开展了社团活动，分别设置了体育类、艺术类、文学类及其它类社团（要求人人参与社团，每人只能选择一项）．为了解学生喜爱哪种社团活动，学校做了一次抽样调查．根据收集到的数据，绘制成如下两幅不完整的统计图，请根据图中提供的信息，完成下列问题：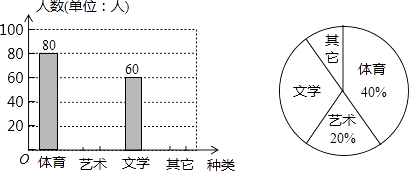
    （1）此次共调查了多少人？
    （2）求文学社团在扇形统计图中所占圆心角的度数；
    （3）请将条形统计图补充完整；
    （4）若该校有1500名学生，请估计喜欢体育类社团的学生有多少人？

    查看答案和解析>>

    同步练习册答案