练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    13．已知点A（1，-1），点B（2，0），点M为横坐标轴上一动点，要使MA=MB，则M的坐标为（1，0）．

    分析 如图，连接AB，由MA=MB，得到点M在线段AB的垂直平分线上由于点M为横坐标轴上一动点，于是得到M的坐标为（1，0）．

    解答 解：如图，连接AB，∵MA=MB，
    ∴点M在线段AB的垂直平分线上，
    ∵点M为横坐标轴上一动点，
    ∴M的坐标为（1，0），
    故答案为：（1，0）．

    点评 本题考查了线段垂直平分线的性质，坐标与图形的性质，熟练掌握各性质是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    3．在△ABC中，∠C=90°，AC=3BC，则sinA=$\frac{\sqrt{10}}{10}$，cosA=$\frac{3\sqrt{10}}{10}$，tanA=$\frac{1}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

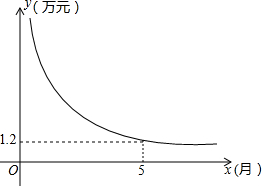    4．黄女士参加了上海通用汽车公司推出的分期付款购买汽车活动，她购买的别克汽车价格为16.3万元，交了首付之后每月付款y万元，x月结清余款，y与x的函数关系如图所示，试根据图象提供的信息回答下列问题．
    （1）确定y与x的函数关系式，并求出首付款的数目；
    （2）这次活动要求顾客最迟在购车后两年内将余款结清，那么黄女士每个月至少要付款多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．如图所示，在△ABC中，AM垂直平分边BC，若AB=3.6cm，则AC=3.6cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

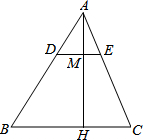    8．如图所示：AH是△ABC的边上的高，M为AH上一点，且AM：MH=1：2，过M引DE∥BC分别交AB，AC于点D，E，若BC=16cm、AH=9cm．
    （1）求△ADE的面积；
    （2）AM：MH为何值时，S△ADE：S平行四边形BDEC=1：1？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．在0.458，4.$\stackrel{•}{2}$，$\frac{π}{2}$，$\sqrt{0.4}$，-$\root{3}{0.001}$，$\frac{1}{7}$这几个数中无理数有2个．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．计算
    （1）（3.14-π）0-2-3+（-4）2÷（$\frac{1}{2}$）-2
    （2）（-3x）3+（x4）2÷（-x）5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

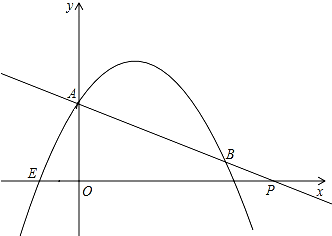    2．如图，在平面直角坐标系中，抛物线y=-$\frac{1}{2}$x2+bx+c的图象过点E（-1，0）、点A（0，2）两点．
    （1）求抛物线的解析式（关系式）；
    （2）直线y=-$\frac{1}{3}$x+2交x轴于点P，交y轴于点A．并与抛物线相交于A、B两点．
    ①在x轴的正半轴上是否存在点M，使得△MAB是直角三角形？若存在，请求出点M的坐标；若不存在，请说明理由；
    ②若抛物线与坐标轴的另一个交点为F，将线段EF在x轴上平移，当线段EF怎样平移时，四边形ABFE的周长最小？求出此时点E、F的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．先化简．再求值：$\frac{3-a}{4-2a}$÷（$\frac{5}{a-2}$-a-2），其中a=-$\frac{6}{3+\sqrt{3}}$．

    查看答案和解析>>

    同步练习册答案