
| A. | 在公园调查了1000名老年人的健康状况 | |
| B. | 在医院调查了1000名老年人的健康状况 | |
| C. | 调查了100名小区内老年邻居的健康状况 | |
| D. | 利用派出所的户籍网随机调查了该地区10%的老年人的健康状况 |
分析 抽取样本注意事项就是要考虑样本具有广泛性与代表性,所谓代表性,就是抽取的样本必须是随机的,即各个方面,各个层次的对象都要有所体现.
解答 解:A、在公园调查了1000名老年人的健康状况,抽查的都是锻炼的老人,没有代表性,故A错误;
B、在医院调查了1000名老年人的健康状况,抽查的都是不健康的老人,没有代表性,故B错误;
C、调查了100名小区内老年邻居的健康状况,调查没有广泛性,故C错误;
D、利用派出所的户籍网随机调查了该地区10%的老年人的健康状况,调查由广泛性、代表性,故D正确;
故选:D.
点评 本题考查了抽样调查的可靠性,样本具有代表性是指抽取的样本必须是随机的,即各个方面,各个层次的对象都要有所体现.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
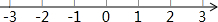 解不等式组$\left\{\begin{array}{l}{x+3>0①}\\{(x-1)≤2x-1②}\end{array}\right.$
解不等式组$\left\{\begin{array}{l}{x+3>0①}\\{(x-1)≤2x-1②}\end{array}\right.$查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6.74×10-5 | B. | 6.74×10-6 | C. | 6.75×10-5 | D. | 6.75×10-6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com