
分析 ①利用整式的乘法和完全平方公式计算,进一步合并,最后代入求得答案即可;
②利用整式的乘法和完全平方公式计算,进一步合并,再用整式的除法计算,最后代入求得答案即可.
解答 解:①原式=x2+4xy-x2+4x-4+4x
=4xy+8x-4
当x=$\frac{1}{16}$,y=-16时,
原式=-4+$\frac{1}{2}$-4=-$\frac{15}{2}$;
②原式=[x2-xy-2y2-x2+4xy-4y2]÷(-3y)
=[3xy-6y2]÷(-3y)
=-x+2y
当x=-1,y=$\frac{1}{2}$时,
原式=1+1=2.
点评 此题考查整式的化简求值,注意先利用整式的乘法和计算公式计算,合并化简后再进一步代入求得数值即可.


科目:初中数学 来源: 题型:选择题
| A. | 在公园调查了1000名老年人的健康状况 | |
| B. | 在医院调查了1000名老年人的健康状况 | |
| C. | 调查了100名小区内老年邻居的健康状况 | |
| D. | 利用派出所的户籍网随机调查了该地区10%的老年人的健康状况 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
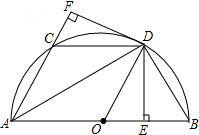 如图,AB是半圆O的直径,AB=a,C是半圆上一点,弦AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,连接CD,DB,OD.
如图,AB是半圆O的直径,AB=a,C是半圆上一点,弦AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,连接CD,DB,OD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
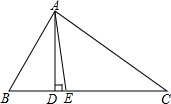 如图,在△ABC中,∠B>∠C,AD⊥BC,AE平分∠BAC,
如图,在△ABC中,∠B>∠C,AD⊥BC,AE平分∠BAC,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com