
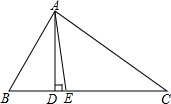
 如图,在△ABC中,∠B>∠C,AD⊥BC,AE平分∠BAC,
如图,在△ABC中,∠B>∠C,AD⊥BC,AE平分∠BAC,分析 (1)根据三角形内角和得出∠BAC,再根据角平分线定义得出∠BAE,利用互余得出∠BAD,最后解答即可;
(2)根据三角形内角和得出∠BAC,再根据角平分线定义得出∠BAE,利用互余得出∠BAD,最后解答即可;
(3)根据三角形内角和得出∠BAC,再根据角平分线定义得出∠BAE,利用互余得出∠BAD,最后解答即可;
(4)由(1)(2)(3)推理可得三者关系.
解答 解:(1)∵∠B=80°,∠C=40°,
∴∠BAC=180°-80°-40°=60°,
∵AE平分∠BAC,
∴∠BAE=30°,
∵AD⊥BC,∠B=80°,
∴∠BAD=10°,
∴∠DAE=30°-10°=20°;
(2)∵∠B=40°,∠C=30°,
∴∠BAC=180°-40°-30°=110°,
∵AE平分∠BAC,
∴∠BAE=55°,
∵AD⊥BC,∠B=40°,
∴∠BAD=50°,
∴∠DAE=55°-50°=5°;
(3)∵∠B-∠C=40°,
∴∠BAC=180°-∠B-(∠B-40°)=140°-2∠B,
∵AE平分∠BAC,
∴∠BAE=70°-∠B,
∵AD⊥BC,
∴∠BAD=90°-∠B,
∴∠DAE=90°-∠B-(70°-∠B)=20°;
(4)由(1)和(2)(3)可得:∠DAE=$\frac{1}{2}$(∠B-∠C);
故答案为:(2)5°;(3)20°;(4)∠DAE=$\frac{1}{2}$(∠B-∠C).
点评 此题考查三角形内角和问题,关键是根据三角形内角和和角平分线的定义进行分析.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
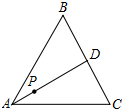 如图,P为等边△ABC的中线AD上一点,AD=3AP,在边AB、AC上分别取点M、N,使△PMN为以MN为底的等腰直角三角形,若AP=1+$\sqrt{3}$,则MN的长为( )
如图,P为等边△ABC的中线AD上一点,AD=3AP,在边AB、AC上分别取点M、N,使△PMN为以MN为底的等腰直角三角形,若AP=1+$\sqrt{3}$,则MN的长为( )| A. | 2 | B. | 4+2$\sqrt{3}$ | C. | 2$\sqrt{2}$+$\sqrt{6}$ | D. | 4+2$\sqrt{3}$或2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
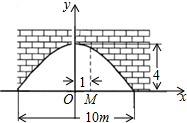 如图,有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为4m,跨度为10m.把它的截面边缘的图形放在如图所示的直角坐标系中.在对称轴右边1m处,桥洞离水面的高是$\frac{99}{25}$m.
如图,有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为4m,跨度为10m.把它的截面边缘的图形放在如图所示的直角坐标系中.在对称轴右边1m处,桥洞离水面的高是$\frac{99}{25}$m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 脐橙品种 | A | B | C |
| 每辆汽车运载(吨) | 10 | 8 | 6 |
| 每吨脐橙所获利润(元) | 600 | 1000 | 800 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com