
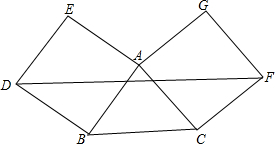
 如图,△ABC的边AB,AC分别向外作正方形ABDE和正方形ACFG,DF∥BC.求证:AB=AC.
如图,△ABC的边AB,AC分别向外作正方形ABDE和正方形ACFG,DF∥BC.求证:AB=AC. 分析 分别过D、A、F作直线BC的垂线,垂足分别为M、H、N,证明Rt△BDM≌Rt△ABH,得到DM=BH,同理FN=CH,根据两平行线间的距离相等得到DM=FN,于是BH=CH,根据线段垂直平分线的性质得出结论.
解答 证明:如图,分别过D、A、F作直线BC的垂线,垂足分别为M、H、N,
∵四边形ABDE是正方形,
∴AB=BD,∠DBA=90°,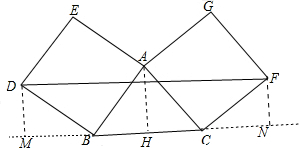
∴∠DBM=90°-∠ABH,
∵∠BAH=90°-∠ABH,
∴∠BAH=∠DBM,
∵DM⊥MB,AH⊥BC,
∴∠DMB=∠BHA,
在Rt△BDM和Rt△ABH中
$\left\{\begin{array}{l}{∠DMB=∠BHA}\\{∠BAH=∠DBM}\\{AB=DB}\end{array}\right.$
∴Rt△BDM≌Rt△ABH
∴DM=BH
同理:FN=CH
∵DF∥BC
∴DM=FN
∴BH=CH
∵AH⊥BC
∴AB=AC.
点评 本题考查了正方形的性质,三角形全等的判定与性质,平行线的性质以及线段垂直平分线的性质,添加辅助线构造全等三角形是解决问题的关键,此题有一定难度.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
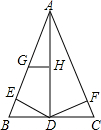 如图,已知AB=AC,AD是中线,BE=CF.
如图,已知AB=AC,AD是中线,BE=CF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
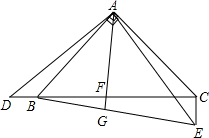 在三角形ABC中,AB=AC,∠BAC=90°,∠DAE=90°.
在三角形ABC中,AB=AC,∠BAC=90°,∠DAE=90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
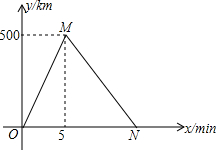 小亮和小华的家住在滨河大道旁,周六早上,他们两个相约去滨河大道上训练跑步,他们从A路口出发,沿滨河大道跑到B路口再原路返回,因为体力的原因,他们返回的平均速度都是各自出发时速度的$\frac{4}{5}$,设出发时间为x min,距A路口的距离为y cm,图中折线表示小亮在整个训练过程中y与x之间的函数关系图象.
小亮和小华的家住在滨河大道旁,周六早上,他们两个相约去滨河大道上训练跑步,他们从A路口出发,沿滨河大道跑到B路口再原路返回,因为体力的原因,他们返回的平均速度都是各自出发时速度的$\frac{4}{5}$,设出发时间为x min,距A路口的距离为y cm,图中折线表示小亮在整个训练过程中y与x之间的函数关系图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知抛物线y=ax2+c与x轴交于点A、B,其中点A的坐标是(-1,0),与y轴交于点N(0,-1).
如图,已知抛物线y=ax2+c与x轴交于点A、B,其中点A的坐标是(-1,0),与y轴交于点N(0,-1).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
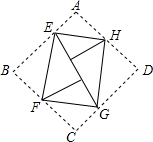 如图,有一个长(AB)为10cm的矩形纸板(即矩形ABCD),现将这个纸板的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH.若EF=8cm,则四边形EFGH的面积为( )
如图,有一个长(AB)为10cm的矩形纸板(即矩形ABCD),现将这个纸板的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH.若EF=8cm,则四边形EFGH的面积为( )| A. | 36cm2 | B. | 48cm2 | C. | 64cm2 | D. | 72cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com