练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．$\frac{1}{c}$+$\frac{1}{d}$=$\frac{1}{m}$（c+d≠0），则m=$\frac{cd}{c+d}$．

    分析 把c与d看做已知数求出m即可．

    解答 解：$\frac{1}{c}$+$\frac{1}{d}$=$\frac{1}{m}$，
    解得：m=$\frac{cd}{c+d}$，
    故答案为：$\frac{cd}{c+d}$

    点评 此题考查了分式的加减法，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

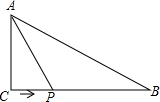    10．如图，在Rt△ABC中，已知∠C=90°，边AC=4cm，BC=5cm，点P为CB边上一点，当动点P沿CB从点C向点B运动时，△APC的面积发生了变化．
    （1）在这个变化过程中，自变量和因变量各是什么？
    （2）如果设CP长为x cm，△APC的面积为y cm，则y与x的关系可表示为y=2x；
    （3）当点P从点D（D为BC的中点）运动到点B时，则△APC的面积从5cm2变到10cm2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．现有一块半径为$\sqrt{2}$R的圆形铁皮，用它裁一块面积最大的正方形铁皮的边长是2R．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．已知a=$\frac{1}{2+\sqrt{7}}$，b=$\frac{1}{2-\sqrt{7}}$，求a3-a+b3-b的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．解方程组$\left\{\begin{array}{l}{x+y+z=3.3}\\{\frac{x}{3}+\frac{y}{4}+\frac{z}{5}=\frac{51}{60}}\\{\frac{x}{5}+\frac{y}{4}+\frac{z}{3}=\frac{53.4}{60}}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．（a+b）（x+y）的积有4项，那么，猜测（a1+a2+…+an）（x1+x2+…+xn）的积有几项？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．已知，关于x的一元二次方程（k-3）x2-2（k2-4）x+3k-k2=0
    （1）k取何值时，有一根为零？
    （2）k取何值时，有两个互为相反数的实数根？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

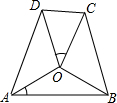    1．如图，O为四边形ABCD内一点，OA=OB=OC=OD，∠AOB与∠CDO互补，∠OAB与∠COD相等，则$\frac{AB}{CD}$==$\frac{3+\sqrt{5}}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．如图是抛物线y=ax2+bx+c（a≠0）的一部分，已知抛物线的对称轴为x=2，与x轴的一个交点是（-1，0）．有下列结论：①abc＞0；②4a+b＜0；③$\frac{c}{a}$=-5；④如果点（3，y1）和点（6，y2）都在抛物线上，那么y1＞y2；⑤方程ax2+bx+c=0的两个根是-1，5．其中正确的结论是（　　）
    A．①②⑤B．②④C．①③⑤D．③④

    查看答案和解析>>

    同步练习册答案