
 一个直立的火柴盒在桌面上倒下,启迪人们发现快乐勾股定理的一种新的证明方法,如图所示,火柴盒的一个侧面ABCD倒下到A′B′C′D′的位置,连接CC′.设AB=a,BC=b,AC=c,请利用此图证明勾股定理:a2+b2=c2.
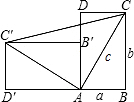
一个直立的火柴盒在桌面上倒下,启迪人们发现快乐勾股定理的一种新的证明方法,如图所示,火柴盒的一个侧面ABCD倒下到A′B′C′D′的位置,连接CC′.设AB=a,BC=b,AC=c,请利用此图证明勾股定理:a2+b2=c2. 分析 四边形BCC′D′的面积从大的一方面来说属于直角梯形,可利用直角梯形的面积公式进行表示从组成来看,由三个直角三角形组成.应利用三角形的面积公式来进行表示.
解答 证明:四边形BCC′D′为直角梯形,
∴S梯形BCC′D′=$\frac{1}{2}$(BC+C′D′)•BD′=$\frac{(a+b)^{2}}{2}$,
又∵∠AB′C′=90°,Rt△ABC≌Rt△AB′C′
∴∠BAC=∠B′AC′.
∴∠CAC′=∠CAB′+∠B′AC′=∠CAB′+∠BAC=90°;
∴S梯形BCC′D′=S△ABC+S△CAC′+S△D′AC′=$\frac{1}{2}$ab+$\frac{1}{2}$c2+$\frac{1}{2}$ab=$\frac{{c}^{2}+2ab}{2}$;
∴$\frac{(a+b)^{2}}{2}$=$\frac{{c}^{2}+2ab}{2}$;
∴a2+b2=c2.
点评 本题考查了勾股定理的证明.证明勾股定理时,需注意:组成的图形的面积有两种表示方法:大的面积的表示方法和各个组成部分的面积的和.


科目:初中数学 来源: 题型:解答题
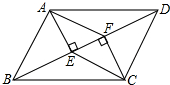 如图,在?ABCD中,BD是对角线,AE⊥BD于点E,CF⊥BD于点F,试判断
如图,在?ABCD中,BD是对角线,AE⊥BD于点E,CF⊥BD于点F,试判断查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com