
【题目】如图,在平面直角坐标系中,点A(0,3),B是x轴正半轴上一动点,将点A绕点B顺时针旋转60°得点C,OB延长线上有一点D,满足∠BDC=∠BAC,则线段BD长为_____.
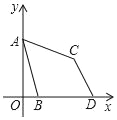
【答案】2![]() .
.
【解析】
如图,在DO上取一点H,使得DH=CD.设AH交BC于点K.只要证明△ACH≌△BCD(SAS),推出∠CAH=∠CBD,AH=BD,由∠AKC=∠BKH,推出∠KHB=∠ACB=60°,求出AH即可解决问题;
解:如图,在DO上取一点H,使得DH=CD.设AH交BC于点K.
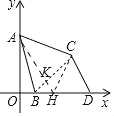
∵BA=BC,∠ABC=60°,
∴△ABC是等边三角形,
∵DC=DH,∠CDH=60°,
∴△CDH是等边三角形,
∴CA=CB,CH=CD,∠ACB=∠HCD=60°,
∴∠ACH=∠BCD,
∴△ACH≌△BCD(SAS),
∴∠CAH=∠CBD,AH=BD,
∵∠AKC=∠BKH,
∴∠KHB=∠ACB=60°,
在Rt△AOH中,∵OA=3,
∴AH=![]() =2
=2![]() ,
,
∴BD=AH=2![]() .
.
故答案为2![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
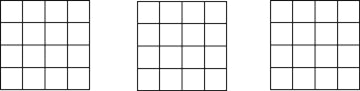
【题目】(1)以下列正方形网络的交点为顶点,分别画出两个相似比不为1的相似三角形,使它们:①都是直角三角形;②都是锐角三角形;③都是钝角三角形.
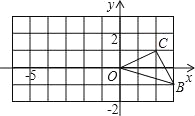
(2)如图,已知O是坐标原点,B、C两点的坐标分别为(3,﹣1)、(2,1).
①以0点为位似中心在y轴的左侧将△OBC放大到两倍(即新图与原图的相似比为2),画出图形;
②分别写出B、C两点的对应点B′、C′的坐标;
③如果△OBC内部一点M的坐标为(x,y),写出M的对应点M′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形OABC的一边OA在x轴上,将菱形OABC绕原点O顺时针旋转75°至OA’B’C’的位置.若OB=![]() ,∠C=120°,则点B’的坐标为( )
,∠C=120°,则点B’的坐标为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】善于归纳和总结的小明发现,“数形结合”是初中数学的基本思想方法,被广泛地应用在数学学习和解决问题中.用数量关系描述图形性质和用图形性质描述数量关系,往往会有新的发现.小明在研究垂直于直径的弦的性质过程中(如图,直径AB⊥弦CD于点E,设AE=x,BE=y,用含x,y的式子表示图中的弦CD的长度),通过比较运动的弦CD和与之垂直的直径AB的大小关系,发现了一个关于正数x,y的不等式,你也能发现这个不等式吗?写出你发现的不等式.
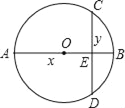
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=3x2+36x+81.
(1)写出它的顶点坐标;
(2)当x取何值时,y随x的增大而增大;
(3)求出图象与x轴的交点坐标;
(4)当x取何值时,y有最小值,并求出最小值;
(5)当x取何值时,y<0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一笔直的海岸线l上有A、B两个观测站,C离海岸线l的距离(即CD的长)为2,从A测得船C在北偏东45°的方向,从B测得船C在北偏东22.5°的方向,则AB的长( )
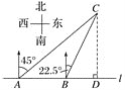
A. 2 km B. (2+![]() )km C. (4-2
)km C. (4-2![]() ) km D. (4-
) km D. (4-![]() ) km
) km
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中装有4张相同的纸牌,它们分别标有数字1,2,3,4.随机地摸取出一张纸牌然后放回,在随机摸取出一张纸牌,(1)计算两次摸取纸牌上数字之和为5的概率;
(2)甲、乙两个人进行游戏,如果两次摸出纸牌上数字之和为奇数,则甲胜;如果两次摸出纸牌上数字之和为偶数,则乙胜.这是个公平的游戏吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=﹣x2+bx+c(c>0)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,且OB=OC=3,顶点为M.
(1)求二次函数的解析式;
(2)点P为线段BM上的一个动点,过点P作x轴的垂线PQ,垂足为Q,若OQ=m,四边形ACPQ的面积为S,求S关于m的函数解析式,并写出m的取值范围;
(3)探索:线段BM上是否存在点N,使△NMC为等腰三角形?如果存在,求出点N的坐标;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥CD,∠A=90°,AB=1,AD=3,DC=5.点S沿A→B→C运动到C点停止,以S为圆心,SD为半径作弧交射线DC于T点,设S点运动的路径长为x,等腰△DST的面积为y,则y与x的函数图象应为( )
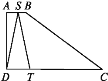
A. 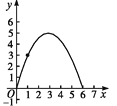 B.
B. 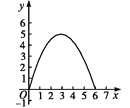
C. 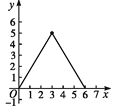 D.
D. 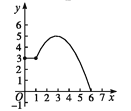
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com