
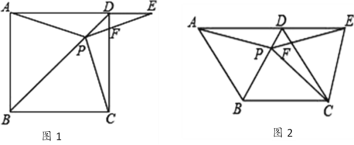
【题目】如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
(1)证明:△APD≌△CPD;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
【答案】(1)证明见解析;(2)90°;(3)AP=CE.
【解析】
(1)利用正方形得到AD=CD,∠ADP=∠CDP=45![]() ,即可证明全等;
,即可证明全等;
(2)设![]() ,利用三角形内角和性质及外角性质得到
,利用三角形内角和性质及外角性质得到![]() ,
,![]() ,再利用周角计算得出x值;
,再利用周角计算得出x值;
(3)AP=CE. 设![]() ,利用三角形内角和性质及外角性质得到
,利用三角形内角和性质及外角性质得到![]() ,
,
![]() ,求出
,求出![]() ,得到
,得到![]() 是等边三角形,即可证得AP=CE.
是等边三角形,即可证得AP=CE.
解:
(1)![]() 四边形ABCD是正方形,
四边形ABCD是正方形,
∴AD=CD,∠ADP=∠CDP=45![]() ,
,
在![]() 与
与![]() 中,
中,
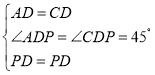 ,
,
∴![]() ;
;
(2)设![]() ,
,
由(1)得,![]() ,
,![]()
因为PA=PE,所以![]()
所以![]() ;
;
(3)AP=CE.
设![]() ,
,
由(1)得,![]() ,
,![]()
∵PA=PE且在菱形ABCD中![]() ,
,
∴![]() ,
,
∴![]() ,
,
由(1)得PA=PC,∴PC=PE,
∴![]() 是等边三角形,
是等边三角形,
∴PE=PC=CE,
∴AP=CE.


科目:初中数学 来源: 题型:
【题目】小明同学在一次社会实践活动中,通过对某种蔬菜在1月份至7月份的市场行情进行统计分析后得出如下规律:
①该蔬菜的销售价![]() (单位:元/千克)与时间
(单位:元/千克)与时间![]() (单位:月份)满足关系:
(单位:月份)满足关系: ![]() ;
;
②该蔬菜的平均成本![]() (单位:元/千克)与时间
(单位:元/千克)与时间![]() (单位:月份)满足二次函数关系
(单位:月份)满足二次函数关系![]() .已知4月份的平均成本为2元/千克,6月份的平均成本为1元/千克.
.已知4月份的平均成本为2元/千克,6月份的平均成本为1元/千克.
(1)求该二次函数的解析式;
(2)请运用小明统计的结论,求出该蔬菜在第几月份的平均利润![]() (单位:元/千克)最大?最大平均利润是多少?(注:平均利润
(单位:元/千克)最大?最大平均利润是多少?(注:平均利润![]() 销售价
销售价![]() 平均成本)
平均成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
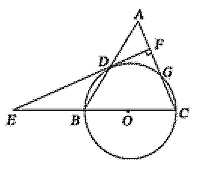
【题目】如图,等腰三角形ABC中,AC=BC=6,AB=8,以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E.
(1)求证:直线EF是⊙O的切线;
(2)求sin∠E的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,D为BC边上一动点,过D作DE⊥AD交AB于E,AC=2,BC=4,当D点从C点运动到B点时,点E运动的路径长为_____.
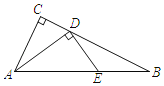
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() x2﹣3x+4与x轴交于A、B两点(A点在B点的左侧),交y轴于点C.
x2﹣3x+4与x轴交于A、B两点(A点在B点的左侧),交y轴于点C.
(1)A点坐标为 ,B点坐标为 ,C点坐标为 ;
(2)如图1,D为B点右侧抛物线上一点,连接AD,若tan∠CAD=2,求D点坐标;
(3)E、F是对称轴右侧第一象限抛物线上的两动点,直线AE、AF分别交y轴于M、N,如图2.若OMON=2,直线EF上有且只有一点P到原点O的距离为定值,求出P点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
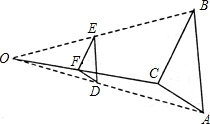
【题目】按如下方法,将△ABC的三边缩小的原来的![]() ,如图,任取一点O,连AO、BO、CO,并取它们的中点D、E、F,得△DEF,则下列说法正确的个数是( )
,如图,任取一点O,连AO、BO、CO,并取它们的中点D、E、F,得△DEF,则下列说法正确的个数是( )
①△ABC与△DEF是位似图形②△ABC与△DEF是相似图形
③△ABC与△DEF的周长比为1:2④△ABC与△DEF的面积比为4:1.
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
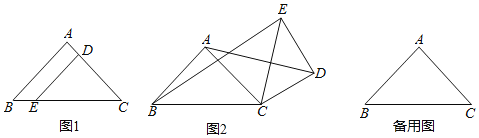
【题目】如图1,在Rt△ABC中,∠BAC=90°,AB=AC,D,E两点分别在AC,BC上,且DE∥AB,将△CDE绕点C按顺时针方向旋转,记旋转角为α.
(1)问题发现:当α=0°时,![]() 的值为 ;
的值为 ;
(2)拓展探究:当0°≤α<360°时,若△EDC旋转到如图2的情况时,求出![]() 的值;
的值;
(3)问题解决:当△EDC旋转至A,B,E三点共线时,若设CE=5,AC=4,直接写出线段BE的长 .
查看答案和解析>>
科目:初中数学 来源: 题型:
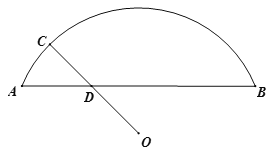
【题目】如图,O是![]() 所在圆的圆心,C是
所在圆的圆心,C是![]() 上一动点,连接OC交弦AB于点D.已知AB=9.35cm,设A,D两点间的距离为
上一动点,连接OC交弦AB于点D.已知AB=9.35cm,设A,D两点间的距离为![]() cm,O,D两点间的距离为
cm,O,D两点间的距离为![]() cm,C,D两点间的距离为
cm,C,D两点间的距离为![]() cm.小腾根据学习函数的经验,分别对函数
cm.小腾根据学习函数的经验,分别对函数![]() ,
,![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究.下面是小腾的探究过程,请补充完整:
的变化而变化的规律进行了探究.下面是小腾的探究过程,请补充完整:
(1)按照下表中自变量![]() 的值进行取点、画图、测量,分别得到了
的值进行取点、画图、测量,分别得到了![]() ,
,![]() 与
与![]() 的几组对应值:
的几组对应值:
| 0.00 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 | 7.10 | 8.00 | 9.35 |
| 4.93 | 3.99 |
| 2.28 | 1.70 | 1.59 | 2.04 | 2.88 | 3.67 | 4.93 |
| 0.00 | 0.94 | 1.83 | 2.65 | 3.23 | 3.34 | 2.89 | 2.05 | 1.26 | 0.00 |
(2)①在同一平面直角坐标系![]() 中,描出表中各组数值所对应的点(
中,描出表中各组数值所对应的点(![]() ,
,![]() ), (
), (![]() ,
,![]() ),并画出(1)中所确定的函数
),并画出(1)中所确定的函数![]() ,
,![]() 的图象;
的图象;
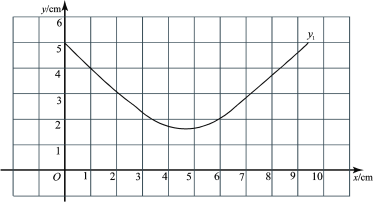
②观察函数![]() 的图象,可得
的图象,可得![]() cm(结果保留一位小数);
cm(结果保留一位小数);
(
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E是AD边的中点,BD,CE交于点H,BE、AH交于点G,则下列结论:①∠ABE=∠DCE;②AG⊥BE;③S△BHE=S△CHD;④∠AHB=∠EHD.其中正确的是( )
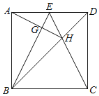
A.①③B.①②③④C.①②③D.①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com