
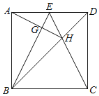
【题目】如图,正方形ABCD中,点E是AD边的中点,BD,CE交于点H,BE、AH交于点G,则下列结论:①∠ABE=∠DCE;②AG⊥BE;③S△BHE=S△CHD;④∠AHB=∠EHD.其中正确的是( )
A.①③B.①②③④C.①②③D.①③④
【答案】B
【解析】
根据正方形的性质证得△BAE≌△CDE,推出∠ABE=∠DCE,可知①正确;利用正方形性质证△ADH≌△CDH,求得∠HAD=∠HCD,推出∠ABE=∠HAD;求出∠ABE+∠BAG=90°;最后在△AGE中根据三角形的内角和是180°求得∠AGE=90°即可得到②正确.根据AD∥BC,求出S△BDE=S△CDE,推出S△BDES△DEH=S△CDES△DEH,即:S△BHE=S△CHD,故③正确;由∠AHD=∠CHD,得到邻补角和对顶角相等得到∠AHB=∠EHD,故④正确;
解:∵四边形ABCD是正方形,E是AD边上的中点,
∴AE=DE,AB=CD,∠BAD=∠CDA=90°,
∴△BAE≌△CDE(SAS),
∴∠ABE=∠DCE,
故①正确;
∵四边形ABCD是正方形,
∴AD=DC,∠ADB=∠CDB=45°,DH=DH,
∴△ADH≌△CDH(SAS),
∴∠HAD=∠HCD,
∵∠ABE=∠DCE
∴∠ABE=∠HAD,
∵∠BAD=∠BAH+∠DAH=90°,
∴∠ABE+∠BAH=90°,
∴∠AGB=180°90°=90°,
∴AG⊥BE,
故②正确;
∵AD∥BC,
∴S△BDE=S△CDE,
∴S△BDES△DEH=S△CDES△DEH,
即:S△BHE=S△CHD,
故③正确;
∵△ADH≌△CDH,
∴∠AHD=∠CHD,
∴∠AHB=∠CHB,
∵∠BHC=∠DHE,
∴∠AHB=∠EHD,
故④正确;
故选:B.


科目:初中数学 来源: 题型:
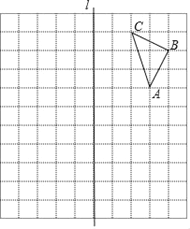
【题目】如图,直线l与△ABC在边长为1个单位长度的小正方形网格中,点A,B,C都为网格线的交点.
(1)请画出△ABC关于直线l对称的△A1B1C1(点A,B,C的对称点分别为A1,B1,C1).
(2)请画出将线段AC向左平移3个单位,再向下平移5个单位得到的线段A2C2(点A,C的对应点分别为A2,C2),再以A2C2为斜边画一个等腰直角三角形A2B2C2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将一块等腰直角三角板(△ABC)按如图所示放置,若AO=2,OC=1,∠ACB=90°.
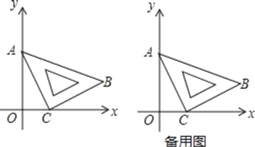
(1)直接写出点B的坐标是 ;
(2)如果抛物线l:y=ax2﹣ax﹣2经过点B,试求抛物线l的解析式;
(3)把△ABC绕着点C逆时针旋转90°后,顶点A的对应点A1是否在抛物线l上?为什么?
(4)在x轴上方,抛物线l上是否存在一点P,使由点A,C,B,P构成的四边形为中心对称图形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O,请用无刻度的直尺完成下列作图.
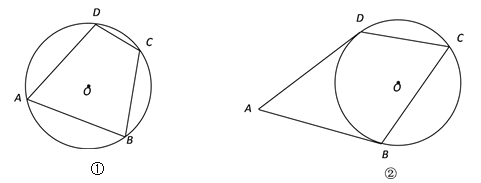
(1)如图①,四边形ABCD是⊙O的内接四边形,且AB=AD,画出∠BCD的角平分线;
(2)如图②,AB和AD是⊙O的切线,切点分别是B、D,点C在⊙O上,画出∠BCD的角平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解题时,最容易想到的方法未必是最简单的,你可以再想一想,尽量优化解法.
例题呈现
关于x的方程a(x+m)2+b=0的解是x1=1,x2=-2(a、m、b均为常数,a≠0),则方程a(x+m+2)2+b=0的解是 .
解法探讨
(1)小明的思路如图所示,请你按照他的思路解决这个问题;
小明的思路
第1步 把1、-2代入到第1个方程中求出m的值;
第2步 把m的值代入到第1个方程中求出![]() 的值;
的值;
第3步 解第2个方程.
(2)小红仔细观察两个方程,她把第2个方程a(x+m+2)2+b=0中的“x+2”看作第1个方程中的“x”,则“x+2”的值为 ,从而更简单地解决了问题.
策略运用
(3)小明和小红认真思考后发现,利用方程结构的特点,无需计算“根的判别式”就能轻松解决以下问题,请用他们说的方法完成解答.
已知方程 (a2-2b2)x2+(2b2-2c2)x+2c2-a2=0有两个相等的实数根,其中a、b、c是△ABC三边的长,判断△ABC的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
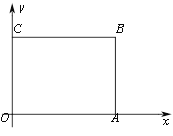
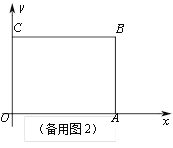
【题目】如图,在直角坐标系中,矩形OABC的边OA在x轴上,OC在y轴上,且B的坐标为(8,6),动点D从B点出发,以1个单位长度每秒的速度向C点运动t秒(D不与B,C重合),连接AD,将△ABD沿AD翻折至△AB'D(B'在矩形的内部或边上),连接DB',DB'所在直线与AC交于点F,与OA所在直线交于点E.
(1)①当t= 秒,B'与F重合;
②求线段CB'的取值范围;
(2)①求EB'的长度(用含t的代数式表示),并求出t的取值范围;
②当t为何值时,△AEF是以AE为底的等腰三角形?并求出此时EC的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数y=![]() 的图象与性质.小美根据学习函数的经验,对函数y=
的图象与性质.小美根据学习函数的经验,对函数y=![]() 的图象与性质进行了探究下面是小美的探究过程,请补充完整:
的图象与性质进行了探究下面是小美的探究过程,请补充完整:
(1)函数y=![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x | -2 | - | -1 | - |
|
| 1 | 2 | 3 | 4 | … |
y | 0 | - | -1 | - |
|
| td style="width:28.95pt; border-top-style:solid; border-top-width:0.75pt; border-right-style:solid; border-right-width:0.75pt; border-left-style:solid; border-left-width:0.75pt; padding:3.38pt 5.03pt; vertical-align:middle">m |
|
| … |
求m的值;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;

(4)结合函数的图象,写出该函数的一条性质: .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com