
ЁОЬтФПЁПНтЬтЪБЃЌзюШнвзЯыЕНЕФЗНЗЈЮДБиЪЧзюМђЕЅЕФЃЌФуПЩвддйЯывЛЯыЃЌОЁСПгХЛЏНтЗЈЃЎ
Р§ЬтГЪЯж
ЙигкxЕФЗНГЬa(xЃЋm)2ЃЋbЃН0ЕФНтЪЧx1ЃН1ЃЌx2ЃНЃ2ЃЈaЁЂmЁЂbОљЮЊГЃЪ§ЃЌaЁй0ЃЉЃЌдђЗНГЬa(xЃЋmЃЋ2)2ЃЋbЃН0ЕФНтЪЧЁЁ ЃЎ
НтЗЈЬНЬж
ЃЈ1ЃЉаЁУїЕФЫМТЗШчЭМЫљЪОЃЌЧыФуАДееЫћЕФЫМТЗНтОіетИіЮЪЬтЃЛ
аЁУїЕФЫМТЗ
Ек1ВН Аб1ЁЂЃ2ДњШыЕНЕк1ИіЗНГЬжаЧѓГіmЕФжЕЃЛ
Ек2ВН АбmЕФжЕДњШыЕНЕк1ИіЗНГЬжаЧѓГі![]() ЕФжЕЃЛ
ЕФжЕЃЛ
Ек3ВН НтЕк2ИіЗНГЬЃЎ
ЃЈ2ЃЉаЁКьзаЯИЙлВьСНИіЗНГЬЃЌЫ§АбЕк2ИіЗНГЬa(xЃЋmЃЋ2)2ЃЋbЃН0жаЕФЁАxЃЋ2ЁБПДзїЕк1ИіЗНГЬжаЕФЁАxЁБЃЌдђЁАxЃЋ2ЁБЕФжЕЮЊЁЁ ЃЌДгЖјИќМђЕЅЕиНтОіСЫЮЪЬтЃЎ
ВпТддЫгУ
ЃЈ3ЃЉаЁУїКЭаЁКьШЯецЫМПМКѓЗЂЯжЃЌРћгУЗНГЬНсЙЙЕФЬиЕуЃЌЮоашМЦЫуЁАИљЕФХаБ№ЪНЁБОЭФмЧсЫЩНтОівдЯТЮЪЬтЃЌЧыгУЫћУЧЫЕЕФЗНЗЈЭъГЩНтД№ЃЎ
вбжЊЗНГЬ (a2Ѓ2b2)x2ЃЋ(2b2Ѓ2c2)xЃЋ2c2Ѓa2ЃН0гаСНИіЯрЕШЕФЪЕЪ§ИљЃЌЦфжаaЁЂbЁЂcЪЧЁїABCШ§БпЕФГЄЃЌХаЖЯЁїABCЕФаЮзДЃЎ
ЁОД№АИЁПЃЈ1ЃЉx1ЃНЃ1ЃЌx2ЃНЃ4 ЃЈ2ЃЉ1ЛђЃ2 ЃЈ3ЃЉжБНЧШ§НЧаЮ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЬтвтРћгУД§ЖЈЯЕЪ§ЗЈЧѓНтМДПЩ.
ЃЈ2ЃЉАбКѓУцвЛИіЗНГЬжаЕФx+2ПДзїећЬхЃЌЯрЕБгкЧАУцвЛИіЗНГЬжаЕФxЧѓНтЃЎ
ЃЈ3ЃЉЯШИљОнгаСНИіЯрЕШЕФЪЕЪ§ИљЃЌдйИљОнИљгкЯЕЪ§ЕФЙиЯЕСаГіЗНГЬЃЌевЕНaЁЂbЁЂcЕФЙиЯЕЃЌДгЖјХаЖЯШ§НЧаЮЕФаЮзДЃЎ
ЃЈ1ЃЉНтЃКНЋx1ЃН1ЃЌx2ЃНЃ2ДњШыЕНЗНГЬa(xЃЋm)2ЃЋbЃН0жаЃЌ
ЕУ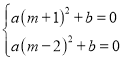 ЃЌ
ЃЌ
Ёр mЃЋ1ЃНЁР(mЃ2)ЃЌ
НтЕУ mЃН![]()
Ёр a(![]() ЃЋ1)2ЃЋbЃН0ЃЎ
ЃЋ1)2ЃЋbЃН0ЃЎ
Ёр Ѓ![]() ЃН
ЃН![]()
Ек2ИіЗНГЬПЩБфаЮЮЊ(xЃЋ![]() ЃЋ2)2ЃНЃ
ЃЋ2)2ЃНЃ![]() ЃЌ
ЃЌ
МД(xЃЋ![]() )2ЃН
)2ЃН![]() ЃЌ
ЃЌ
НтЕУЃКx1ЃНЃ1ЃЌx2ЃНЃ4
ЃЈ2ЃЉЙигкxЕФЗНГЬaЃЈx+mЃЉ2+b=0ЕФНтЪЧx1=-2ЃЌx2=1ЃЌЃЈaЃЌmЃЌbОљЮЊГЃЪ§ЃЌaЁй0ЃЉЃЛ
ЃЈ3ЃЉНтЃКЁп (a2Ѓ2b2)ЃЋ(2b2Ѓ2c2)ЃЋ(2c2Ѓa2)ЃН0ЃЌ
Ёр ЗНГЬБигавЛИљЪЧxЃН1
Ёр ЗНГЬЕФСНИљЮЊx1ЃНx2ЃН1ЃЎ
Ёр x1ЁЄx2ЃН1ЃН![]() ЃЎ
ЃЎ
Ёр a2ЃНb2ЃЋc2ЃЎ
Ёр ЁїABCЪЧвЛИіжБНЧШ§НЧаЮ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌABЃНACЃЌADЁЭBCДЙзуЪЧDЃЌANЪЧЁЯBACЕФЭтНЧЁЯCAMЕФЦНЗжЯпЃЌCEЁЭANЃЌДЙзуЪЧEЃЌСЌНгDEНЛACгкFЃЎ
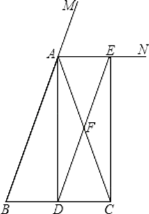
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮADCEЮЊОиаЮЃЛ
ЃЈ2ЃЉЧѓжЄЃКDFЁЮABЃЌDFЃН![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЕБЁїABCТњзуЪВУДЬѕМўЪБЃЌЫФБпаЮADCEЮЊе§ЗНаЮЃЌМђЪіФуЕФРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
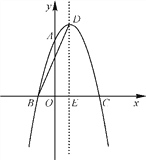
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпyЃНax2ЃЋ2xЃЋcОЙ§ЕуA(0ЃЌ3)ЃЌB(Ѓ1ЃЌ0)ЃЌЧыЛиД№ЯТСаЮЪЬтЃК
(1)ЧѓХзЮяЯпЖдгІЕФЖўДЮКЏЪ§ЕФБэДяЪНЃЛ
(2)ХзЮяЯпЕФЖЅЕуЮЊDЃЌЖдГЦжсгыxжсНЛгкЕуEЃЌСЌНгBDЃЌЧѓBDЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮABCDжаЃЌЕуEЪЧADБпЕФжаЕуЃЌBDЃЌCEНЛгкЕуHЃЌBEЁЂAHНЛгкЕуGЃЌдђЯТСаНсТлЃКЂйЁЯABEЃНЁЯDCEЃЛЂкAGЁЭBEЃЛЂлSЁїBHEЃНSЁїCHDЃЛЂмЁЯAHBЃНЁЯEHDЃЎЦфжае§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
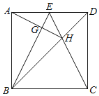
A.ЂйЂлB.ЂйЂкЂлЂмC.ЂйЂкЂлD.ЂйЂлЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЙигкxЕФвЛдЊЖўДЮЗНГЬ kx2ЃЋ(2kЃЋ1)xЃЋkЃЋ2ЃН0ЃЎ
ЃЈ1ЃЉШєИУЗНГЬгаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЌЧѓkЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉШєИУЗНГЬЕФСНИљx1ЁЂx2Тњзу![]() ЃНЃ3ЃЌЧѓkЕФжЕЃЎ
ЃНЃ3ЃЌЧѓkЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкМзввСНИіВЛЭИУїЕФПкДќжаЃЌЗжБ№гаДѓаЁЁЂВФжЪЭъШЋЯрЭЌЕФаЁЧђЃЌЦфжаМзПкДќжаЕФаЁЧђЩЯЗжБ№БъгаЪ§зж1ЃЌ2ЃЌ3ЃЌ4ЃЌввПкДќжаЕФаЁЧђЩЯЗжБ№БъгаЪ§зж2ЃЌ3ЃЌ4ЃЌЯШДгМзДќжаШЮвтУўГівЛИіаЁЧђЃЌМЧЯТЪ§зжЮЊmЃЌдйДгввДќжаУўГівЛИіаЁЧђЃЌМЧЯТЪ§зжЮЊnЃЎ
ЃЈ1ЃЉЧыгУСаБэЛђЛЪїзДЭМЕФЗНЗЈБэЪОГіЫљгаЃЈmЃЌnЃЉПЩФмЕФНсЙћЃЛ
ЃЈ2ЃЉШєmЃЌnЖМЪЧЗНГЬx2Љ5x+6ЃН0ЕФНтЪБЃЌдђаЁУїЛёЪЄЃЛШєmЃЌnЖМВЛЪЧЗНГЬx2Љ5x+6ЃН0ЕФНтЪБЃЌдђаЁРћЛёЪЄЃЌЮЪЫћУЧСНШЫЫЛёЪЄЕФИХТЪДѓЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮABCDжаЃЌMЮЊBCЩЯвЛЕуЃЌMEЁЭAMЃЌMEНЛADЕФбгГЄЯпгкЕуEЃЎ

ЃЈ1ЃЉЧѓжЄЃКЁїABM ЁзЁїEMAЃЛ
ЃЈ2ЃЉШєABЃН2ЃЌBMЃН1ЃЌЧѓDEЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
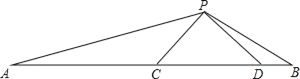
ЁОЬтФПЁПШчЭМЃКЁїPCDЪЧЕШбќжБНЧШ§НЧаЮЃЌЁЯDPC=90ЁуЃЌЁЯAPB=135Ёу
ЧѓжЄЃКЃЈ1ЃЉЁїPACЁзЁїBPDЃЛ
ЃЈ2ЃЉШєAC=3ЃЌBD=1ЃЌЧѓCDЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕФкЃЌвддЕуOЮЊдВаФЃЌ1ЮЊАыОЖзїдВЃЌЕуPдкжБЯп![]() ЩЯдЫЖЏЃЌЙ§ЕуPзїИУдВЕФвЛЬѕЧаЯпЃЌЧаЕуЮЊAЃЌдђPAЕФзюаЁжЕЮЊ
ЩЯдЫЖЏЃЌЙ§ЕуPзїИУдВЕФвЛЬѕЧаЯпЃЌЧаЕуЮЊAЃЌдђPAЕФзюаЁжЕЮЊ![]() ЁЁЁЁ
ЁЁЁЁ![]()
A. 3 B. 2 C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com