
【题目】如图,正方形ABCD中,M为BC上一点,ME⊥AM,ME交AD的延长线于点E.

(1)求证:△ABM ∽△EMA;
(2)若AB=2,BM=1,求DE的长.
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
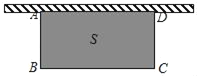
【题目】如图.利用一面墙(墙的长度不限),用20m的篱笆围成一个矩形场地ABCD.设矩形与墙垂直的一边AB=xm,矩形的面积为Sm2.
(1)用含x的式子表示S;
(2)若面积S=48m2,求AB的长;
(3)能围成S=60m2的矩形吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O,请用无刻度的直尺完成下列作图.
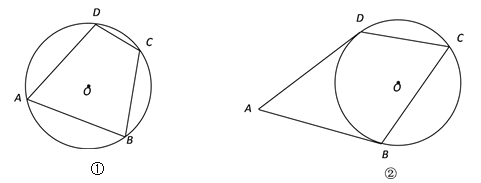
(1)如图①,四边形ABCD是⊙O的内接四边形,且AB=AD,画出∠BCD的角平分线;
(2)如图②,AB和AD是⊙O的切线,切点分别是B、D,点C在⊙O上,画出∠BCD的角平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解题时,最容易想到的方法未必是最简单的,你可以再想一想,尽量优化解法.
例题呈现
关于x的方程a(x+m)2+b=0的解是x1=1,x2=-2(a、m、b均为常数,a≠0),则方程a(x+m+2)2+b=0的解是 .
解法探讨
(1)小明的思路如图所示,请你按照他的思路解决这个问题;
小明的思路
第1步 把1、-2代入到第1个方程中求出m的值;
第2步 把m的值代入到第1个方程中求出![]() 的值;
的值;
第3步 解第2个方程.
(2)小红仔细观察两个方程,她把第2个方程a(x+m+2)2+b=0中的“x+2”看作第1个方程中的“x”,则“x+2”的值为 ,从而更简单地解决了问题.
策略运用
(3)小明和小红认真思考后发现,利用方程结构的特点,无需计算“根的判别式”就能轻松解决以下问题,请用他们说的方法完成解答.
已知方程 (a2-2b2)x2+(2b2-2c2)x+2c2-a2=0有两个相等的实数根,其中a、b、c是△ABC三边的长,判断△ABC的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,OA是⊙O的半径,以OA为直径的⊙C与⊙O的弦AB相交于点D,连结OD并延长交⊙O于点E,连结AE.
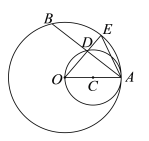
(1)求证:AD=DB.
(2)若AO=10,DE=4,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
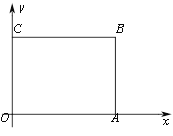
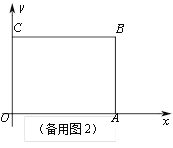
【题目】如图,在直角坐标系中,矩形OABC的边OA在x轴上,OC在y轴上,且B的坐标为(8,6),动点D从B点出发,以1个单位长度每秒的速度向C点运动t秒(D不与B,C重合),连接AD,将△ABD沿AD翻折至△AB'D(B'在矩形的内部或边上),连接DB',DB'所在直线与AC交于点F,与OA所在直线交于点E.
(1)①当t= 秒,B'与F重合;
②求线段CB'的取值范围;
(2)①求EB'的长度(用含t的代数式表示),并求出t的取值范围;
②当t为何值时,△AEF是以AE为底的等腰三角形?并求出此时EC的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种成本为40元![]() 千克的商品,若按50元
千克的商品,若按50元![]() 千克销售,一个月可售出500千克,现打算涨价销售,据市场调查,涨价x元时,月销售量为m千克,m是x的一次函数,部分数据如下表:
千克销售,一个月可售出500千克,现打算涨价销售,据市场调查,涨价x元时,月销售量为m千克,m是x的一次函数,部分数据如下表:

![]() 观察表中数据,直接写出m与x的函数关系式:_______________:当涨价5元时,计算可得月销售利润是___________元;
观察表中数据,直接写出m与x的函数关系式:_______________:当涨价5元时,计算可得月销售利润是___________元;
![]() 当售价定多少元时,会获得月销售最大利润,求出最大利润.
当售价定多少元时,会获得月销售最大利润,求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2+2x﹣3.
(1)把函数配成y=a(x﹣h)2+k的形式;
(2)求函数与x轴交点坐标;
(3)用五点法画函数图象
x | … | … | |||||
y | … | … |
(4)当y>0时,则x的取值范围为_____.
(5)当﹣3<x<0时,则y的取值范围为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某新建火车站站前广场需要绿化的面积为46000米2,施工队在绿化了22000米2后,将每天的工作量增加为原来的1.5倍,结果提前4天完成了该项绿化工程.
(1)该项绿化工程原计划每天完成多少米2?
(2)该项绿化工程中有一块长为20米,宽为8米的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为56米2,两块绿地之间及周边留有宽度相等的人行通道(如图所示),问人行通道的宽度是多少米?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com