
【题目】已知:如图,OA是⊙O的半径,以OA为直径的⊙C与⊙O的弦AB相交于点D,连结OD并延长交⊙O于点E,连结AE.
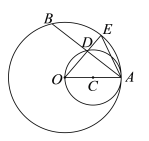
(1)求证:AD=DB.
(2)若AO=10,DE=4,求AE的长.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
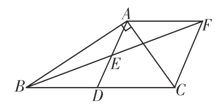
【题目】如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)求证:四边形ADCF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程 kx2+(2k+1)x+k+2=0.
(1)若该方程有两个不相等的实数根,求k的取值范围;
(2)若该方程的两根x1、x2满足![]() =-3,求k的值.
=-3,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,OC是⊙O的半径,点D是半圆AB上一动点(不与A、B重合),连结DC交直径AB与点E,若∠AOC=60°,则∠AED的范围为( )
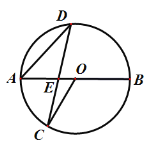
A.0°< ∠AED <180°B.30°< ∠AED <120°
C.60°< ∠AED <120°D.60°< ∠AED <150°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,M为BC上一点,ME⊥AM,ME交AD的延长线于点E.

(1)求证:△ABM ∽△EMA;
(2)若AB=2,BM=1,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于![]() 的方程
的方程![]() .
.
(1)若该方程有两个相等的实数根,求![]() 的值;
的值;
(2)求证:不论![]() 为何值,该方程一定有一个实数根是2;
为何值,该方程一定有一个实数根是2;
(3)若![]() 、
、![]() 是该方程的两个根,且
是该方程的两个根,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.
(1)在图1中证明CE=CF;
(2)若∠ABC=90°,G是EF的中点(如图2),直接写出∠BDG的度数;
(3)若∠ABC=120°,FG∥CE,FG=CE,分别连接DB、DG(如图3),求∠BDG的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为菱形,以AD为直径作⊙O交AB于点F,连接DB交⊙O于点H,E是BC上的一点,且BE=BF,连接DE.
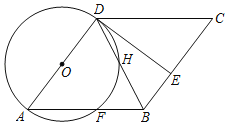
(1)求证:DE是⊙O的切线.
(2)若BF=2,BD=2![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com