
【题目】如图,四边形ABCD为菱形,以AD为直径作⊙O交AB于点F,连接DB交⊙O于点H,E是BC上的一点,且BE=BF,连接DE.
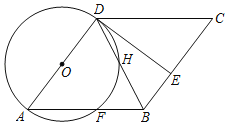
(1)求证:DE是⊙O的切线.
(2)若BF=2,BD=2![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)证明△DAF≌△DCE,可得∠DFA=∠DEC,证出∠ADE=∠DEC=90°,即OD⊥DE,DE是⊙O的切线.
(2)在Rt△ADF和Rt△BDF中,可得AD2-(AD-BF)2=DB2-BF2,解方程可求出AD的长即可.
(1)证明:如图1,连接DF,

∵四边形ABCD为菱形,
∴AB=BC=CD=DA,AD∥BC,∠DAB=∠C,
∵BF=BE,
∴AB﹣BF=BC﹣BE,
即AF=CE,
∴△DAF≌△DCE(SAS),
∴∠DFA=∠DEC,
∵AD是⊙O的直径,
∴∠DFA=90°,
∴∠DEC=90°
∵AD∥BC,
∴∠ADE=∠DEC=90°,
∴OD⊥DE,
∵OD是⊙O的半径,
∴DE是⊙O的切线;
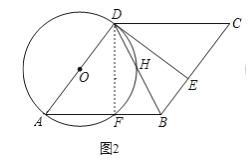
(2)解:如图2,
∵AD是⊙O的直径,
∴∠DFA=90°,
∴∠DFB=90°,
在Rt△ADF和Rt△BDF中,
∵DF2=AD2﹣AF2,DF2=BD2﹣BF2,
∴AD2﹣AF2=DB2﹣BF2,
∴AD2﹣(AD﹣BF)2=DB2﹣BF2,
∴![]()
∴AD=5.
∴⊙O的半径为![]() .
.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】随着《流浪地球》的热播,其同名科幻小说的销量也急剧上升.为应对这种变化,某网店分别花20000元和30000元先后两次增购该小说,第二次的数量比第一次多500套,且两次进价相同.
(1)该科幻小说第一次购进多少套?
(2)根据以往经验:当销售单价是25元时,每天的销售量是250套;销售单价每上涨1元,每天的销售量就减少10套.网店要求每套书的利润不低于10元且不高于18元.
①直接写出网店销售该科幻小说每天的销售量y(套)与销售单价x(元)之间的函数关系式及自变量x的取值范围;
②网店决定每销售1套该科幻小说,就捐赠a(0<a<7)元给困难职工,每天扣除捐赠后可获得的最大利润为1960元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象交
的图象交![]() 轴于
轴于![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() 的坐标为
的坐标为![]() .
.

(1)求二次函数的解析式和直线![]() 的解析式;
的解析式;
(2)点![]() 是直线
是直线![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴的垂线,交抛物线于点
轴的垂线,交抛物线于点![]() ,当点
,当点![]() 在第一象限时,求线段
在第一象限时,求线段![]() 长度的最大值;
长度的最大值;
(3)在抛物线上是否存在异于![]() 的点
的点![]() ,使
,使![]() 中
中![]() 边上的高为
边上的高为![]() ,若存在求出点
,若存在求出点![]() 的坐标;若不存在请说明理由.
的坐标;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
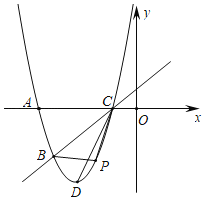
【题目】如图,已知抛物线![]() 经过
经过![]() ,
,![]() 两点,与x轴的另一个交点为C,顶点为D,连结CD.
两点,与x轴的另一个交点为C,顶点为D,连结CD.
(1)求该抛物线的表达式;
(2)点P为该抛物线上一动点(与点B、C不重合),设点P的横坐标为t.
①当点P在直线BC的下方运动时,求![]() 的面积的最大值;
的面积的最大值;
②该抛物线上是否存在点P,使得![]() 若存在,求出所有点P的坐标;若不存在,请说明理由.
若存在,求出所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
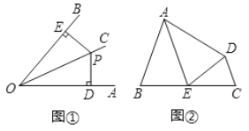
【题目】教材呈现:下图是华师版八年级上册数学教材第96页的部分内容.
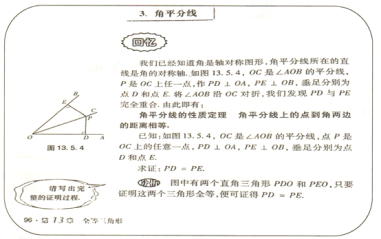
请根据教材中的分析,结合图①,写出“角平分线的性质定理”完整的证明过程.
定理应用:
如图②,在四边形![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上.
上.![]() 平分
平分![]() ,
,![]() 平分
平分![]() .
.
(1)求证:![]() .
.
(2)若![]() ,
,![]() ,则
,则![]() 的长为______.
的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
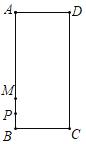
【题目】如图,矩形ABCD中,动点P沿B→A→D→C→B路线运动,点M是AB边上的一点,且MB=![]() AB,已知AB=4,BC=2,AP=2MP,则点P到边AD的距离为_______.
AB,已知AB=4,BC=2,AP=2MP,则点P到边AD的距离为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
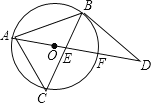
【题目】如图,点O为△ABC外接圆的圆心,以AB为腰作等腰△ABD,使底边AD经过点O,并分别交BC于点E、交⊙O于点F,若∠BAD=30°.
(1)求证:BD是⊙O的切线;
(2)当CA2=CECB时,
①求∠ABC的度数;
②![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为边在
为边在![]() 的另一侧作
的另一侧作![]() ,点
,点![]() 为射线
为射线![]() 上任意一点,在射线
上任意一点,在射线![]() 上截取
上截取![]() ,连接
,连接![]() .
.
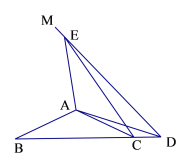
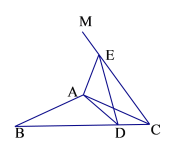
(1)如图1,当点![]() 落在线段
落在线段![]() 的延长线上时,直接写出
的延长线上时,直接写出![]() 的度数;
的度数;
(2)如图2,当点![]() 落在线段
落在线段![]() (不含边界)上时,
(不含边界)上时,![]() 与
与![]() 于点
于点![]() ,请问(1)中的结论是否仍成立?如果成立,请给出证明;如果不成立,请说明理由;
,请问(1)中的结论是否仍成立?如果成立,请给出证明;如果不成立,请说明理由;
(3)在(2)的条件下,若![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市用3400元购进A、B两种文具盒共120个,这两种文具盒的进价、标价如下表:
价格/类型 | A型 | B型 |
进价(元/只) | 15 | 35 |
标价(元/只) | 25 | 50 |
(1)这两种文具盒各购进多少只?
(2)若A型文具盒按标价的9折出售,B型文具盒按标价的8折出售,那么这批文具盒全部售出后,超市共获利多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com