
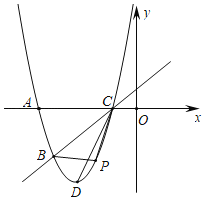
【题目】如图,已知抛物线![]() 经过
经过![]() ,
,![]() 两点,与x轴的另一个交点为C,顶点为D,连结CD.
两点,与x轴的另一个交点为C,顶点为D,连结CD.
(1)求该抛物线的表达式;
(2)点P为该抛物线上一动点(与点B、C不重合),设点P的横坐标为t.
①当点P在直线BC的下方运动时,求![]() 的面积的最大值;
的面积的最大值;
②该抛物线上是否存在点P,使得![]() 若存在,求出所有点P的坐标;若不存在,请说明理由.
若存在,求出所有点P的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②存在,
;②存在,![]() 或
或![]() .
.
【解析】
(1)将点A、B坐标代入二次函数表达式,即可求解;
(2)①![]() ,即可求解;②分点P在直线BC下方、上方两种情况,分别求解即可.
,即可求解;②分点P在直线BC下方、上方两种情况,分别求解即可.
解:(1)将点A、B坐标代入二次函数表达式得:![]() ,解得:
,解得:![]() ,
,
故抛物线的表达式为:![]() …①,
…①,
令![]() ,则
,则![]() 或
或![]() ,
,
即点![]() ;
;
(2)①如图1,过点P作y轴的平行线交BC于点G,
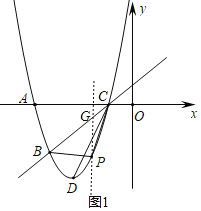
将点B、C的坐标代入一次函数表达式并解得:
直线BC的表达式为:![]() …②,
…②,
设点![]() ,则点
,则点![]() ,
,
![]() ,
,
![]() ,
,![]() 有最大值,当
有最大值,当![]() 时,其最大值为
时,其最大值为![]() ;
;
②设直线BP与CD交于点H,
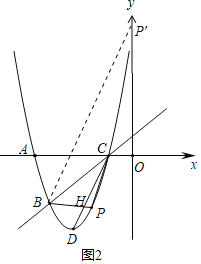
当点P在直线BC下方时,
![]() ,
,![]() 点H在BC的中垂线上,
点H在BC的中垂线上,
线段BC的中点坐标为![]() ,
,
过该点与BC垂直的直线的k值为﹣1,
设BC中垂线的表达式为:![]() ,将点
,将点![]() 代入上式并解得:
代入上式并解得:
直线BC中垂线的表达式为:![]() …③,
…③,
同理直线CD的表达式为:![]() …④,
…④,
联立③④并解得:![]() ,即点
,即点![]() ,
,
同理可得直线BH的表达式为:![]() …⑤,
…⑤,
联立①⑤并解得:![]() 或
或![]() (舍去
(舍去![]() ),
),
故点![]() ;
;
当点![]() 在直线BC上方时,
在直线BC上方时,
![]() ,
,![]() ,
,
则直线BP′的表达式为:![]() ,将点B坐标代入上式并解得:
,将点B坐标代入上式并解得:![]() ,
,
即直线BP′的表达式为:![]() …⑥,
…⑥,
联立①⑥并解得:![]() 或
或![]() (舍去
(舍去![]() ),
),
故点![]() ;
;
故点P的坐标为![]() 或
或![]() .
.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
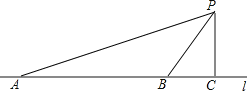
【题目】汽车超速行驶是交通安全的重大隐患,为了有效降低交通事故的发生,许多道路在事故易发路段设置了区间测速如图,学校附近有一条笔直的公路l,其间设有区间测速,所有车辆限速40千米/小时数学实践活动小组设计了如下活动:在l上确定A,B两点,并在AB路段进行区间测速.在l外取一点P,作PC⊥l,垂足为点C.测得PC=30米,∠APC=71°,∠BPC=35°.上午9时测得一汽车从点A到点B用时6秒,请你用所学的数学知识说明该车是否超速.(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,sin71°≈0.95,cos71°≈0.33,tan71°≈2.90)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax22a2x(a![]() 0)的对称轴与x轴交于点P.
0)的对称轴与x轴交于点P.
(1)求点P的坐标(用含a的代数式表示);
(2)记函数y=x+2(1![]() x
x![]() 2)的图象为图形M,若抛物线与图形M恰有一个公共点,结合函数的图象,求a的取值范围.
2)的图象为图形M,若抛物线与图形M恰有一个公共点,结合函数的图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(0,1).
(1)画出△ABC向右平移3个单位长度所得的△A1B1C1;写出C1点的坐标;
(2)画出将△ABC绕点B按逆时针方向旋转90°所得的△A2B2C2;写出C2点的坐标;
(3)在(2)的条件下求点A所经过路径的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
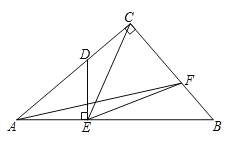
【题目】如图,在Rt△ABC中,∠ACB=90°,点D在AC上,DE⊥AB于点E,且CD=DE.点F在BC上,连接EF,AF,若∠CEF=45°,∠B=2∠CAF,BF=2,则AB的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级计划成立学生社团,要求每一位学生都选择一个社团而且只能选择一个社团.为了解学生对不同社团的选择意向,随机抽取了七年级部分学生进行“我最喜爱的社团”问卷调查,并将调查结果绘制成如下两个不完整的统计图表.
七年级部分学生“我最喜爱的社团”调查结果统计表
社团名称 | 人数 |
文学社团 | 4 |
创客社团 | 9 |
书法社团 |
|
绘画社团 | 6 |
体育社团 | 10 |
音乐社团 | 5 |
美食社团 |
|
数学社团 | 2 |
七年级部分学生“我最喜爱的社团”调查结果扇形统计图
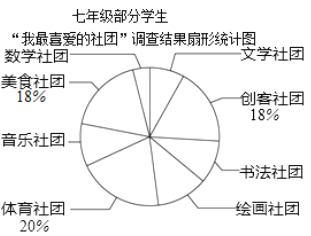
请解答下列问题:
(1)![]() ______,
______,![]() ______.
______.
(2)在扇形统计图中,“绘画社团”所对应的扇形圆心角为______度.
(3)该校七年级共有350名学生,每个社团人数不低于30人才可以开展.试通过计算估计该校七年级有哪些社团可以开展.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为菱形,以AD为直径作⊙O交AB于点F,连接DB交⊙O于点H,E是BC上的一点,且BE=BF,连接DE.
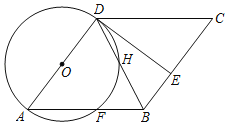
(1)求证:DE是⊙O的切线.
(2)若BF=2,BD=2![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】刘徵是我国古代最杰出的数学家之一,他在《九算术圆田术)中用“割圆术”证明了圆面积的精确公式,并给出了计算圆周率的科学方法(注:圆周率=圆的周长与该圆直径的比值)“割圆术”就是以“圆内接正多边形的面积”,来无限逼近“圆面积”,刘徽形容他的“割圆术”说:割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣.刘徽计算圆周率是从正六边形开始的,易知圆的内接正六边形可分为六个全等的正三角形,每个三角形的边长均为圆的半径R.此时圆内接正六边形的周长为6R,如果将圆内接正六边形的周长等同于圆的周长,可得圆周率为3.当正十二边形内接于圆时,如果按照上述方法计算,可得圆周率为_____.(参考数据:sinl5°=0.26)
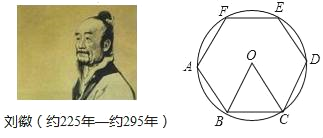
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com