
【题目】在平面直角坐标系xOy中,抛物线y=ax22a2x(a![]() 0)的对称轴与x轴交于点P.
0)的对称轴与x轴交于点P.
(1)求点P的坐标(用含a的代数式表示);
(2)记函数y=x+2(1![]() x
x![]() 2)的图象为图形M,若抛物线与图形M恰有一个公共点,结合函数的图象,求a的取值范围.
2)的图象为图形M,若抛物线与图形M恰有一个公共点,结合函数的图象,求a的取值范围.
【答案】(1)(a,0);(2)a≤![]() 或a>0
或a>0
【解析】
(1)令y=0,求得抛物线与x轴的两个交点坐标,进而求得点P坐标;
(2)根据抛物线与图形M恰有一个公共点,结合图像可知当x=-1或当x=2时,这两个函数值的大小关系恰好相反,然后通过解不等式组即可求得a的取值范围.
解:(1)y=ax22a2x=ax(x2a)
令y=0,则x1=0,x2=2a,
∴对称轴为x=![]() ,
,
∴点P的坐标为(a,0)
(2)设y1=ax22a2x,y2=x+2(1![]() x
x![]() 2)
2)
∴当x=-1时,y1=a+2a2,y2=3,
当x=2时,y1=4a-4a2,y2=0,
∵抛物线与图形M恰有一个公共点,
∴抛物线与图形M如图所示:
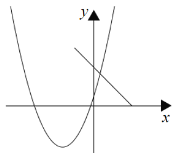


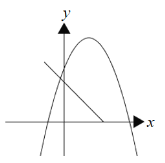
∴当a+2a2≥3时,4a-4a2≤0,
则2a2+a-3≥0,4a2-4a≥0,
∴(2a+3)(a-1)≥0①,4a(a-1)≥0②,
∴由①得,a≥1或a≤![]() ,
,
由②得,a≥1或a≤0,
∴a≥1或a≤![]() ,
,
当a+2a2≤3时,4a-4a2≥0,
则2a2+a-3≤0,4a2-4a≤0,
∴(2a+3)(a-1)≤0①,4a(a-1)≤0②,
∴由①得,![]() ≤a≤1,
≤a≤1,
由②得,0≤a≤1,
∴0≤a≤1,
∴a≤![]() 或a≥0,
或a≥0,
又∵a≠0,
∴a的取值范围是:a≤或a>0.


科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN.
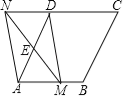
(1)求证:四边形AMDN是平行四边形.
(2)当AM的值为何值时,四边形AMDN是矩形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着《流浪地球》的热播,其同名科幻小说的销量也急剧上升.为应对这种变化,某网店分别花20000元和30000元先后两次增购该小说,第二次的数量比第一次多500套,且两次进价相同.
(1)该科幻小说第一次购进多少套?
(2)根据以往经验:当销售单价是25元时,每天的销售量是250套;销售单价每上涨1元,每天的销售量就减少10套.网店要求每套书的利润不低于10元且不高于18元.
①直接写出网店销售该科幻小说每天的销售量y(套)与销售单价x(元)之间的函数关系式及自变量x的取值范围;
②网店决定每销售1套该科幻小说,就捐赠a(0<a<7)元给困难职工,每天扣除捐赠后可获得的最大利润为1960元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
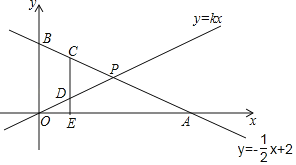
【题目】在平面直角坐标系中,一次函数y=﹣![]() x+2的图象交x轴、y轴分别于A、B两点,交直线y=kx于P.
x+2的图象交x轴、y轴分别于A、B两点,交直线y=kx于P.
(1)求点A、B的坐标;
(2)若OP=PA,求k的值;
(3)在(2)的条件下,C是线段BP上一点,CE⊥x轴于E,交OP于D,若CD=2ED,求C点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
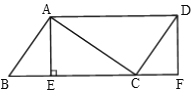
【题目】如图,在平行四边形ABCD中,AE⊥BC于E,点F在BC延长线上,且CF=BE,连接AC,DF,
(1)求证:四边形AEFD是矩形;
(2)若∠ACD=90°,CF=3,DF=4,求AD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象交
的图象交![]() 轴于
轴于![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() 的坐标为
的坐标为![]() .
.

(1)求二次函数的解析式和直线![]() 的解析式;
的解析式;
(2)点![]() 是直线
是直线![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴的垂线,交抛物线于点
轴的垂线,交抛物线于点![]() ,当点
,当点![]() 在第一象限时,求线段
在第一象限时,求线段![]() 长度的最大值;
长度的最大值;
(3)在抛物线上是否存在异于![]() 的点
的点![]() ,使
,使![]() 中
中![]() 边上的高为
边上的高为![]() ,若存在求出点
,若存在求出点![]() 的坐标;若不存在请说明理由.
的坐标;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
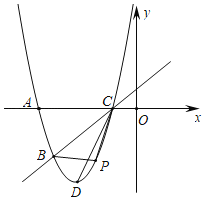
【题目】如图,已知抛物线![]() 经过
经过![]() ,
,![]() 两点,与x轴的另一个交点为C,顶点为D,连结CD.
两点,与x轴的另一个交点为C,顶点为D,连结CD.
(1)求该抛物线的表达式;
(2)点P为该抛物线上一动点(与点B、C不重合),设点P的横坐标为t.
①当点P在直线BC的下方运动时,求![]() 的面积的最大值;
的面积的最大值;
②该抛物线上是否存在点P,使得![]() 若存在,求出所有点P的坐标;若不存在,请说明理由.
若存在,求出所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为边在
为边在![]() 的另一侧作
的另一侧作![]() ,点
,点![]() 为射线
为射线![]() 上任意一点,在射线
上任意一点,在射线![]() 上截取
上截取![]() ,连接
,连接![]() .
.
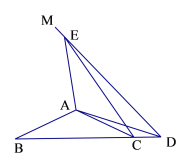
(1)如图1,当点![]() 落在线段
落在线段![]() 的延长线上时,直接写出
的延长线上时,直接写出![]() 的度数;
的度数;
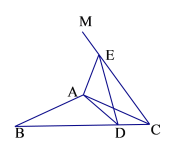
(2)如图2,当点![]() 落在线段
落在线段![]() (不含边界)上时,
(不含边界)上时,![]() 与
与![]() 于点
于点![]() ,请问(1)中的结论是否仍成立?如果成立,请给出证明;如果不成立,请说明理由;
,请问(1)中的结论是否仍成立?如果成立,请给出证明;如果不成立,请说明理由;
(3)在(2)的条件下,若![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com