
【题目】随着《流浪地球》的热播,其同名科幻小说的销量也急剧上升.为应对这种变化,某网店分别花20000元和30000元先后两次增购该小说,第二次的数量比第一次多500套,且两次进价相同.
(1)该科幻小说第一次购进多少套?
(2)根据以往经验:当销售单价是25元时,每天的销售量是250套;销售单价每上涨1元,每天的销售量就减少10套.网店要求每套书的利润不低于10元且不高于18元.
①直接写出网店销售该科幻小说每天的销售量y(套)与销售单价x(元)之间的函数关系式及自变量x的取值范围;
②网店决定每销售1套该科幻小说,就捐赠a(0<a<7)元给困难职工,每天扣除捐赠后可获得的最大利润为1960元,求a的值.
【答案】(1)该科幻小说第一次购进1000套;(2)①y=﹣10x+500(30≤x≤38);②a=2
【解析】
(1)设该科幻小说第一次购进m套,根据题意列方程即可得到结论;
(2)根据题意列函数关系式即可;
(3)设每天扣除捐赠后可获得利润为w元.根据题意得到w=(x-20-a)(-10x+500)=-10x2+(10a+700)x﹣500a﹣10000(30≤x≤38)求得对称轴为x=35+![]() a,
a,
①若0<a<6,则![]() ,则当x=35+
,则当x=35+![]() a时,w取得最大值,解方程得到a1=2,a2=58,于是得到a=2;
a时,w取得最大值,解方程得到a1=2,a2=58,于是得到a=2;
②若6<a<7,则38<35![]() a,则当30≤x≤38时,w随x的增大而增大;解方程得到a=
a,则当30≤x≤38时,w随x的增大而增大;解方程得到a=![]() ,但6<a<7,故舍去.于是得到结论.
,但6<a<7,故舍去.于是得到结论.
解:(1)设该科幻小说第一次购进![]() 套,
套,
则![]() ,
,
![]() ,
,
经检验,当![]() 时,
时,![]() ,则
,则![]() 是原方程的解,
是原方程的解,
答:该科幻小说第一次购进1000套;
(2)根据题意得,![]() ;
;
(3)设每天扣除捐赠后可获得利润为![]() 元.
元.
![]()
对称轴为![]() ,
,
①若![]() ,则
,则![]() ,则当
,则当![]() 时,
时,![]() 取得最大值,
取得最大值,
![]()
![]() ,
,![]() ,
,
又![]() ,则
,则![]() ;
;
②若![]() ,则
,则![]() ,则当
,则当![]() 时,
时,![]() 随
随![]() 的增大而增大;
的增大而增大;
![]() 当
当![]() 时,
时,![]() 取得最大值,则
取得最大值,则![]() ,
,
![]() ,但
,但![]() ,故舍去.
,故舍去.
综上所述,![]() .
.


科目:初中数学 来源: 题型:
【题目】在新的教学改革的推动下,某中学初三年级积极推进走班制教学.为了了解一段时间以来“至善班”的学习效果,年级组织了多次定时测试,现随机选取甲、乙两个“至善班”,从中各抽取20名同学在某一次定时测试中的数学成绩,其结果记录如下:
收集数据:
“至善班”甲班的20名同学的数学成绩统计(满分为100分)(单位:分):86 90 60 76 92 83 56 76 85 70 96 96 90 68 78 80 68 96 85 81
“至善班”乙班的20名同学的数学成绩统计(满分为100分)(单位:分):78 96 75 76 82 87 60 54 87 72 100 82 78 86 70 92 76 80 98 78
整理数据:(成绩得分用x表示)
分数 数量 班级 | 0≤x<60 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x<100 |
甲班(人数) | 1 | 3 | 4 | 6 | 6 |
乙班(人数) | 1 | 1 | 8 | 6 | 4 |
分析数据,并回答下列问题:
(1)完成下表:
平均数 | 中位数 | 众数 | |
甲班 | 80.6 | 82 | a= |
乙班 | 80.35 | b= | 78 |
(2)在“至善班”甲班的扇形图中,成绩在70≤x<80的扇形中,所对的圆心角α的度数为 ,估计全部“至善班”的1600人中优秀人数为 人.(成绩大于等于80分为优秀)
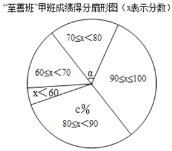
(3)根据以上数据,你认为“至善班” 班(填“甲”或“乙”)所选取做样本的同学的学习效果更好一些,你所做判断的理由是:① ;② .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一组数据a、b、c的平均数为5,方差为4,那么数据a+2、b+2、c+2的平均数和方差分别为( )
A. 7,6 B. 7,4 C. 5,4 D. 以上都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汽车超速行驶是交通安全的重大隐患,为了有效降低交通事故的发生,许多道路在事故易发路段设置了区间测速如图,学校附近有一条笔直的公路l,其间设有区间测速,所有车辆限速40千米/小时数学实践活动小组设计了如下活动:在l上确定A,B两点,并在AB路段进行区间测速.在l外取一点P,作PC⊥l,垂足为点C.测得PC=30米,∠APC=71°,∠BPC=35°.上午9时测得一汽车从点A到点B用时6秒,请你用所学的数学知识说明该车是否超速.(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,sin71°≈0.95,cos71°≈0.33,tan71°≈2.90)
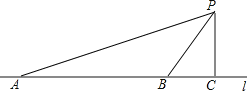
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=3x与反比例函数y=![]() (k>0)的图象交于A,B两点,点P在以C(﹣3,0)为圆心,1为半径的⊙C上,Q是AP的中点,已知OQ长的最大值为2,则k的值为____.
(k>0)的图象交于A,B两点,点P在以C(﹣3,0)为圆心,1为半径的⊙C上,Q是AP的中点,已知OQ长的最大值为2,则k的值为____.
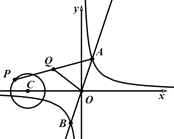
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在半径为5的⊙O中,弦AB=8,P是弦AB所对的优弧上的动点,连接AP,过点A作AP的垂线交射线PB于点C,当△PAB是等腰三角形时,线段BC的长为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
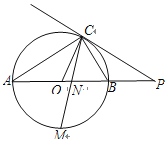
(1)求证:PC是⊙O的切线;
(2)求证:BC=![]() AB;
AB;
(3)点M是弧AB的中点,CM交AB于点N,若AB=4,求MN![]() MC的值.
MC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax22a2x(a![]() 0)的对称轴与x轴交于点P.
0)的对称轴与x轴交于点P.
(1)求点P的坐标(用含a的代数式表示);
(2)记函数y=x+2(1![]() x
x![]() 2)的图象为图形M,若抛物线与图形M恰有一个公共点,结合函数的图象,求a的取值范围.
2)的图象为图形M,若抛物线与图形M恰有一个公共点,结合函数的图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为菱形,以AD为直径作⊙O交AB于点F,连接DB交⊙O于点H,E是BC上的一点,且BE=BF,连接DE.
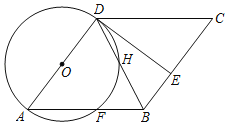
(1)求证:DE是⊙O的切线.
(2)若BF=2,BD=2![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com