
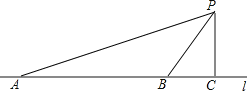
【题目】汽车超速行驶是交通安全的重大隐患,为了有效降低交通事故的发生,许多道路在事故易发路段设置了区间测速如图,学校附近有一条笔直的公路l,其间设有区间测速,所有车辆限速40千米/小时数学实践活动小组设计了如下活动:在l上确定A,B两点,并在AB路段进行区间测速.在l外取一点P,作PC⊥l,垂足为点C.测得PC=30米,∠APC=71°,∠BPC=35°.上午9时测得一汽车从点A到点B用时6秒,请你用所学的数学知识说明该车是否超速.(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,sin71°≈0.95,cos71°≈0.33,tan71°≈2.90)
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系![]() 中,
中,![]() ,
,![]() ,
,![]() 是线段
是线段![]() 上靠近点
上靠近点![]() 的三等分点.
的三等分点.

(1)若点![]() 是
是![]() 轴上的一动点,连接
轴上的一动点,连接![]() 、
、![]() ,当
,当![]() 的值最小时,求出点
的值最小时,求出点![]() 的坐标及
的坐标及![]() 的最小值;
的最小值;
(2)如图2,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,再将
,再将![]() 绕点
绕点![]() 作顺时针方向旋转,旋转角度为
作顺时针方向旋转,旋转角度为![]() ,记旋转中的三角形为
,记旋转中的三角形为![]() ,在旋转过程中,直线
,在旋转过程中,直线![]() 与直线
与直线![]() 的交点为
的交点为![]() ,直线
,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,当
,当![]() 为等腰三角形时,请直接写出
为等腰三角形时,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
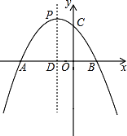
【题目】如图,已知抛物线y=﹣x2﹣2x+m+1与x轴交于A(x1 , 0)、B(x2 , 0)两点,且x1<0,x2>0,与y轴交于点C,顶点为P.(提示:若x1 , x2是一元二次方程ax2+bx+c=0(a≠0)的两个实根,则x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]() )
)
(1)求m的取值范围;
(2)若OA=3OB,求抛物线的解析式;
(3)在(2)中抛物线的对称轴PD上,存在点Q使得△BQC的周长最短,试求出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,新生活超市在端午节前夕购进价格为3元/个的某品牌粽子,根据市场预测,该品牌粽子每个售价4元时,每天能出售500个,并且售价每上涨0.1元,其销售量将减少10个,为了维护消费者利益,物价部门规定,该品牌粽子售价不能超过进价的200%,请你利用所学知识帮助超市给该品牌粽子定价,使超市每天的销售利润为800元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() ,若a,b,c满足b=a+c,则称抛物线
,若a,b,c满足b=a+c,则称抛物线![]() 为“恒定”抛物线.
为“恒定”抛物线.
(1)求证:“恒定”抛物线![]() 必过x轴上的一个定点A;
必过x轴上的一个定点A;
(2)已知“恒定”抛物线![]() 的顶点为P,与x轴另一个交点为B,是否存在以Q为顶点,与x轴另一个交点为C的“恒定”抛物线,使得以PA,CQ为边的四边形是平行四边形?若存在,求出抛物线解析式;若不存在,请说明理由.
的顶点为P,与x轴另一个交点为B,是否存在以Q为顶点,与x轴另一个交点为C的“恒定”抛物线,使得以PA,CQ为边的四边形是平行四边形?若存在,求出抛物线解析式;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
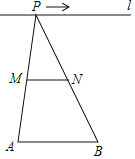
【题目】如图,已知线段![]() ,
,![]() 是直线
是直线![]() 上一动点,点
上一动点,点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,对下列各值:①线段
的中点,对下列各值:①线段![]() 的长;②
的长;②![]() 的周长;③
的周长;③![]() 的面积;④直线
的面积;④直线![]() ,
,![]() 之间的距离;⑤
之间的距离;⑤![]() 的大小.其中不会随点
的大小.其中不会随点![]() 的移动而改变的是_____.(填序号)
的移动而改变的是_____.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
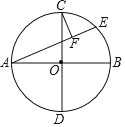
【题目】如图,在⊙O 中,AB、CD是互相垂直的两条直径,点E在![]() 上,CF⊥AE 于点F,若点F四等分弦AE,且AE=8,则⊙O 的面积为______.
上,CF⊥AE 于点F,若点F四等分弦AE,且AE=8,则⊙O 的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对称轴为直线![]() 的抛物线
的抛物线![]() 与x轴相交于A、B两点,其中A点的坐标为(-3,0)。
与x轴相交于A、B两点,其中A点的坐标为(-3,0)。

(1)求点B的坐标;
(2)已知![]() ,C为抛物线与y轴的交点。
,C为抛物线与y轴的交点。
①若点P在抛物线上,且![]() ,求点P的坐标;
,求点P的坐标;
②设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com