
����Ŀ��ijУ���꼶�ƻ�����ѧ�����ţ�Ҫ��ÿһλѧ����ѡ��һ�����Ŷ���ֻ��ѡ��һ�����ţ�Ϊ�˽�ѧ���Բ�ͬ���ŵ�ѡ�����������ȡ�����꼶����ѧ������������ϲ�����������ʾ����飬�������������Ƴ�����������������ͳ��ͼ����
���꼶����ѧ��������ϲ����������������ͳ�Ʊ�
�������� | ���� |
��ѧ���� | 4 |
�������� | 9 |
�鷨���� |
|
�滭���� | 6 |
�������� | 10 |
�������� | 5 |
��ʳ���� |
|
��ѧ���� | 2 |
���꼶����ѧ��������ϲ��������������������ͳ��ͼ
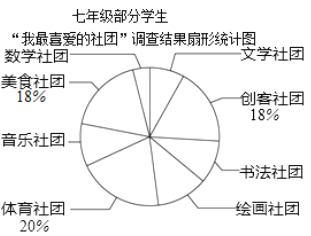
�����������⣺
��1��![]() ______��
______��![]() ______��
______��
��2��������ͳ��ͼ�У����滭����������Ӧ������Բ�Ľ�Ϊ______�ȣ�
��3����У���꼶����350��ѧ����ÿ����������������30�˲ſ��Կ�չ����ͨ��������Ƹ�У���꼶����Щ���ſ��Կ�չ��
���𰸡���1��5��9����2��43.2����3���������š��鷨���š��滭���š��������š��������š���ʳ�����⼸�����ſ��Կ�չ��
��������
��1�����ݴ������ŵ���������ռ�İٷֱȿ�����ñ��ε�����������Ӷ����Եõ�a��b��ֵ��
��2������ͳ�Ʊ��е����ݿ������������ͳ��ͼ�У����滭���š�����Ӧ������Բ�ĽǵĶ�����
��3������ͳ�Ʊ��е����ݿ��Լ������ѧ���Ų��ܿ�չ���������ţ����Կ�չ���ٽ��ͳ�Ʊ��е����ݼ����жϣ�
�⣺��1�����γ���ѧ���У�9��18%��50���ˣ���
b��50��18%��9��a��5049610529��5��
�ʴ�Ϊ��5��9��
��2��������ͳ��ͼ�У����滭����������Ӧ������Բ�Ľ�Ϊ��360���![]() ��43.2����
��43.2����
�ʴ�Ϊ��43.2��
��3����ѧ�����У�350��![]() ��28��30�����ܿ�չ��
��28��30�����ܿ�չ��
���������У�350��![]() ��35��30�����Կ�չ��
��35��30�����Կ�չ��
��ͳ�Ʊ��е����ݿ�֪���������š��鷨���š��滭���š��������š��������š���ʳ���ŵ���������5�˻�5�����ϣ�
����Կ�չ�������ǣ��������š��鷨���š��滭���š��������š��������š���ʳ���ţ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ѱ˸���ȫ��ͬ��С��ƽ��Ϊ���飬ÿ����ÿ���ֱ�д��1��2��3��4�ĸ����֣�Ȼ��ֱ�װ�벻���Ŀڴ��ڽ��ȣ��ӵ�һ���ڴ���ȡ��һ�����������ֺ���Ϊ��P�ĺ�����x��Ȼ���ٴӵڶ����ڴ���ȡ��һ����������ֺ���Ϊ��P�������꣬���P��x��y������ֱ��y=��x+5�ϵĸ����ǣ� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾΪ���κ���![]() ��ͼ�������н���
��ͼ�������н���
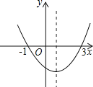
��![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��![]() �����������
�����������
��![]() ��
��
�ܷ���![]() �ĸ���
�ĸ���![]() ��
��
����ȷ�ĸ�����( )����
A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��������y=ax2+bx-3��x�ύ��A��-1��0����B��3��0�����㣬��y�ύ�ڵ�C��
��1���������ߵĽ���ʽ��
��2����ͼ��ֱ��BC�·�������������һ��D������D��DE��BC�ڵ�E����DFƽ��x�ύֱ��BC�ڵ�F�����DEF�ܳ������ֵ��
��3����֪��M�������ߵĶ��㣬��N��y����һ�㣬��Q������ƽ����һ�㣬����P����������һ�㣬��λ�������߶Գ�����Ҳ࣬�Ƿ�����Ե�P��M��N��QΪ��������PMΪ�ߵ������Σ������ڣ���ֱ��д����P�ĺ����ꣻ�������ڣ���˵�����ɣ�
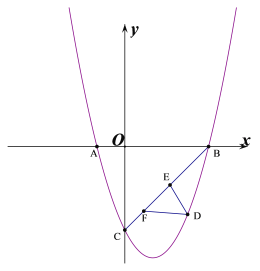
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������![]() ����
����![]() ��
��![]() ���㣬��x�����һ������ΪC������ΪD������CD��
���㣬��x�����һ������ΪC������ΪD������CD��
��1����������ߵı���ʽ��
��2����PΪ����������һ���㣨���B��C���غϣ������P�ĺ�����Ϊt��
�ٵ���P��ֱ��BC���·��˶�ʱ����![]() ����������ֵ��
����������ֵ��
�ڸ����������Ƿ���ڵ�P��ʹ��![]() �����ڣ�������е�P�����ꣻ�������ڣ���˵�����ɣ�
�����ڣ�������е�P�����ꣻ�������ڣ���˵�����ɣ�
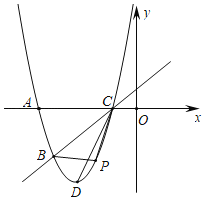
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ʻ��������ͨ�¹ʵ���Ҫԭ������ĩ��С������λͬѧ�������Լ���ѧ��֪ʶ���٣���ͼ���۲�����ڵ��سdz��ϴ���ľ���Ϊ![]() �ĵ�
�ĵ�![]() ������ʱ��һ�����������������ʻ����ô˳���
������ʱ��һ�����������������ʻ����ô˳���![]() ����ʻ��
����ʻ��![]() �����õ�ʱ��Ϊ
�����õ�ʱ��Ϊ![]() �룬��
�룬��![]() ��
��![]() ��
��

![]() ��
��![]() ��
��![]() ֮���·�̣�
֮���·�̣�
![]() ���жϴ˳���Ƿ��˳��ϴ��ÿСʱ
���жϴ˳���Ƿ��˳��ϴ��ÿСʱ![]() ǧ�������ٶȣ�
ǧ�������ٶȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
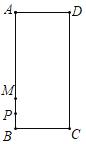
����Ŀ����ͼ������ABCD�У�����P��B��A��D��C��B·���˶�����M��AB���ϵ�һ�㣬��MB��![]() AB����֪AB��4��BC��2��AP��2MP�����P����AD�ľ���Ϊ_______��
AB����֪AB��4��BC��2��AP��2MP�����P����AD�ľ���Ϊ_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
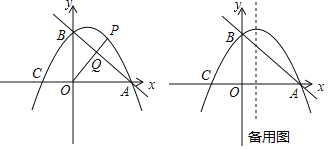
����Ŀ����ͼ��ֱ��y=��![]() x+3��x�ύ�ڵ�A����y�ύ�ڵ�B��������y=��
x+3��x�ύ�ڵ�A����y�ύ�ڵ�B��������y=��![]() x2+bx+c����A��B���㣬��x�����һ������ΪC��
x2+bx+c����A��B���㣬��x�����һ������ΪC��
��1���������ߵĽ���ʽ��
��2����P�ǵ�һ�����������ϵĵ㣬����OP��ֱ��AB�ڵ�Q�����P�ĺ�����Ϊm��PQ��OQ�ı�ֵΪy����y��m�Ĺ�ϵʽ�������PQ��OQ�ı�ֵ�����ֵ��
��3����D�������߶Գ����ϵ�һ���㣬����OD��CD������ODC���Բ��Բ��ΪM����sin��ODC��ֵ���ʱ�����M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͬʱ������ö�ʵؾ��ȵ������������ӣ����Ӹ�����ĵ����ֱ���1��4��������������ö�������µ���ĵ�����Ϊ��a��b�������е�һö���ӵĵ�����Ϊa���ڶ�ö���ӵĵ�����Ϊb��
��1�����оٷ�����״ͼ����a��b���Ľ���ж����֣�
��2����x2+bx+a��0��ʵ����ĸ��ʣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com