
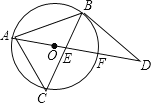
【题目】如图,点O为△ABC外接圆的圆心,以AB为腰作等腰△ABD,使底边AD经过点O,并分别交BC于点E、交⊙O于点F,若∠BAD=30°.
(1)求证:BD是⊙O的切线;
(2)当CA2=CECB时,
①求∠ABC的度数;
②![]() 的值.
的值.
【答案】(1)证明见解析;(2)①∠ABC=45°;②![]() =
=![]() .
.
【解析】
(1)由等腰三角形的性质可得∠D=∠BAD=30°=∠ABO,由外角性质可得∠BOD=60°,即可得∠OBD=90°,可得结论;
(2)①由题意可证△ACE∽△BCA,可得∠CAE=∠ABC=∠CBF,由圆周角定理可求∠ABC的度数;
②通过证明△ACE∽△BFE,可得![]() =
=![]() .
.
(1)连接OB,
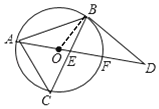
∵△ABD是等腰三角形,∠BAD=30°
∴∠D=∠BAD=30°
∵OA=OB
∴∠BAD=∠ABO=30°
∴∠BOD=60°
∴∠OBD=90°,
即OB⊥BD
∴BD是⊙O的切线;
(2)①连接BF
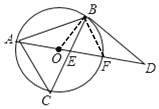
∵AF是直径
∴∠ABF=90°
∵CA2=CECB
∴![]() 且∠C=∠C
且∠C=∠C
∴△ACE∽△BCA
∴∠CAE=∠ABC
∵∠CAE=∠CBF
∴∠ABC=∠CBF,且∠ABF=90°
∴∠ABC=45°
②连接OC
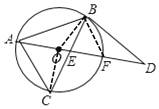
∵∠CAF=∠ABC=45°,AO=CO
∴∠CAF=∠ACO=45°,∠AOC=90°
∴AC=![]() OA
OA
∵∠BOF=60°,OF=OB
∴△OBF是等边三角形
∴BF=OF=OB
∵∠CAF=∠CBF,∠AFB=∠ACB
∴△ACE∽△BFE
∴![]() =
=![]()


 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
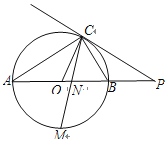
(1)求证:PC是⊙O的切线;
(2)求证:BC=![]() AB;
AB;
(3)点M是弧AB的中点,CM交AB于点N,若AB=4,求MN![]() MC的值.
MC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
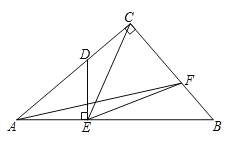
【题目】如图,在Rt△ABC中,∠ACB=90°,点D在AC上,DE⊥AB于点E,且CD=DE.点F在BC上,连接EF,AF,若∠CEF=45°,∠B=2∠CAF,BF=2,则AB的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为菱形,以AD为直径作⊙O交AB于点F,连接DB交⊙O于点H,E是BC上的一点,且BE=BF,连接DE.
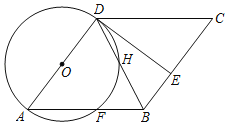
(1)求证:DE是⊙O的切线.
(2)若BF=2,BD=2![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有红、黄两个布袋,红布袋中有两个完全相同的小球,分别标有数字2和4.黄布袋中有三个完全相同的小球,分别标有数字﹣2,﹣4和﹣6.小贤先从红布袋中随机取出一个小球,记录其标有的数字为x,再从黄布袋中随机取出一个小球,记录其标有的数字为y,这样就确定点M的一个坐标为(x.y)
(1)用列表或画树状图的方法写出点M的所有可能坐标;
(2)求点M落在双曲线y=![]() 上的概率.
上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】刘徵是我国古代最杰出的数学家之一,他在《九算术圆田术)中用“割圆术”证明了圆面积的精确公式,并给出了计算圆周率的科学方法(注:圆周率=圆的周长与该圆直径的比值)“割圆术”就是以“圆内接正多边形的面积”,来无限逼近“圆面积”,刘徽形容他的“割圆术”说:割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣.刘徽计算圆周率是从正六边形开始的,易知圆的内接正六边形可分为六个全等的正三角形,每个三角形的边长均为圆的半径R.此时圆内接正六边形的周长为6R,如果将圆内接正六边形的周长等同于圆的周长,可得圆周率为3.当正十二边形内接于圆时,如果按照上述方法计算,可得圆周率为_____.(参考数据:sinl5°=0.26)
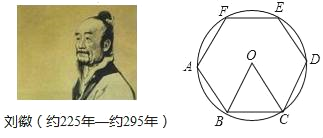
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形![]() 的顶点
的顶点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴正半轴上,点
轴正半轴上,点![]() 在第三象限的双曲线
在第三象限的双曲线![]() 上,过点
上,过点![]() 作
作![]() 轴交双曲线于点
轴交双曲线于点![]() ,连接
,连接![]() ,则
,则![]() 的面积为__________.
的面积为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正偶数按下表排成5列:
第一列 | 第二列 | 第三列 | 第四列 | 第五列 | |
第一行 | 2 | 4 | 6 | 8 | |
第二行 | 16 | 14 | 12 | 10 | |
第三行 | 18 | 20 | 22 | 24 | |
第四行 | 32 | 30 | 28 | 26 | |
…… |
根据上面规律,2020应在( )
A.125行,3列B.125行,2列C.253行,2列D.253行,3列
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在一次数学兴趣小组活动中,对一个数学问题作如下探究:
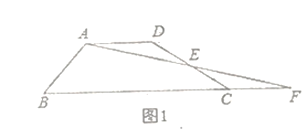
问题情境:(1)如图1,四边形![]() 中,
中,![]() ,点
,点![]() 为
为![]() 边的中点,连接
边的中点,连接![]() 并延长交
并延长交![]() 的延长线于点
的延长线于点![]() ,求证:
,求证:![]() ;(
;(![]() 表示面积)
表示面积)
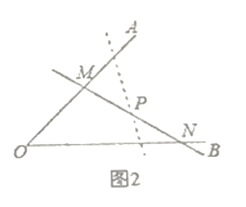
问题迁移:(2)如图2:在已知锐角![]() 内有一个定点
内有一个定点![]() .过点
.过点![]() 任意作一条直线
任意作一条直线![]() 分别交射线
分别交射线![]() 于点
于点![]() .小明将直线
.小明将直线![]() 绕着点
绕着点![]() 旋转的过程中发现,
旋转的过程中发现,![]() 的面积存在最小值,请问当直线
的面积存在最小值,请问当直线![]() 在什么位置时,
在什么位置时,![]() 的面积最小,并说明理由.
的面积最小,并说明理由.
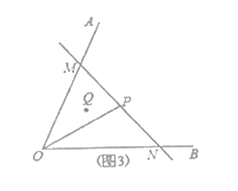
实际应用:(3)如图3,若在道路![]() 之间有一村庄
之间有一村庄![]() 发生疫情,防疫部门计划以公路
发生疫情,防疫部门计划以公路![]() 和经过防疫站
和经过防疫站![]() 的一条直线
的一条直线![]() 为隔离线,建立个面积最小的三角形隔离区
为隔离线,建立个面积最小的三角形隔离区![]() ,若测得
,若测得![]() 试求
试求![]() 的面积.(结果保留根号)(参考数据:
的面积.(结果保留根号)(参考数据:![]() )
)
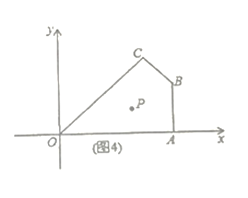
拓展延伸:(4)如图4,在平面直角坐标系中,![]() 为坐标原点,点
为坐标原点,点![]() 的坐标分别为
的坐标分别为![]() ,过点
,过点![]() 的直线
的直线![]() 与四边形
与四边形![]() 一组对边相交,将四边形
一组对边相交,将四边形![]() 分成两个四边形,求其中以点
分成两个四边形,求其中以点![]() 为顶点的四边形面积的最大值.
为顶点的四边形面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com