
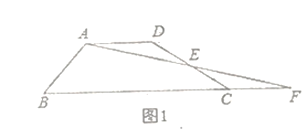
【题目】小明在一次数学兴趣小组活动中,对一个数学问题作如下探究:
问题情境:(1)如图1,四边形![]() 中,
中,![]() ,点
,点![]() 为
为![]() 边的中点,连接
边的中点,连接![]() 并延长交
并延长交![]() 的延长线于点
的延长线于点![]() ,求证:
,求证:![]() ;(
;(![]() 表示面积)
表示面积)
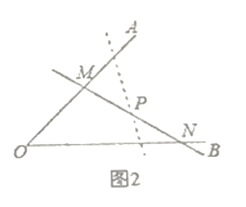
问题迁移:(2)如图2:在已知锐角![]() 内有一个定点
内有一个定点![]() .过点
.过点![]() 任意作一条直线
任意作一条直线![]() 分别交射线
分别交射线![]() 于点
于点![]() .小明将直线
.小明将直线![]() 绕着点
绕着点![]() 旋转的过程中发现,
旋转的过程中发现,![]() 的面积存在最小值,请问当直线
的面积存在最小值,请问当直线![]() 在什么位置时,
在什么位置时,![]() 的面积最小,并说明理由.
的面积最小,并说明理由.
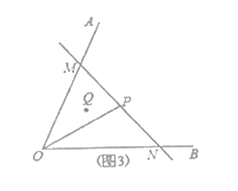
实际应用:(3)如图3,若在道路![]() 之间有一村庄
之间有一村庄![]() 发生疫情,防疫部门计划以公路
发生疫情,防疫部门计划以公路![]() 和经过防疫站
和经过防疫站![]() 的一条直线
的一条直线![]() 为隔离线,建立个面积最小的三角形隔离区
为隔离线,建立个面积最小的三角形隔离区![]() ,若测得
,若测得![]() 试求
试求![]() 的面积.(结果保留根号)(参考数据:
的面积.(结果保留根号)(参考数据:![]() )
)
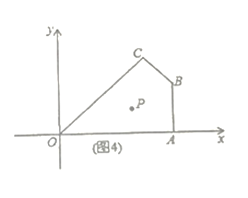
拓展延伸:(4)如图4,在平面直角坐标系中,![]() 为坐标原点,点
为坐标原点,点![]() 的坐标分别为
的坐标分别为![]() ,过点
,过点![]() 的直线
的直线![]() 与四边形
与四边形![]() 一组对边相交,将四边形
一组对边相交,将四边形![]() 分成两个四边形,求其中以点
分成两个四边形,求其中以点![]() 为顶点的四边形面积的最大值.
为顶点的四边形面积的最大值.
【答案】(1)证明见解析;(2)当直线旋转到点![]() 是
是![]() 的中点时
的中点时![]() 最小;(3)
最小;(3)![]() ;(4)10.
;(4)10.
【解析】
(1)根据可以求得△ADE≌△FCE,就可以得出S△ADE=S△FCE就可以得出结论;
(2)根据问题情境的结论可以得出当直线旋转到点P是MN的中点时S△MON最小,过点M作MG∥OB交EF于G.由全等三角形的性质可以得出结论;
(3)如图3,作PP1⊥OB,MM1⊥OB,垂足分别为P1,M1,再根据条件由三角函数值就可以求出结论;
(4)分情况讨论当过点P的直线l与四边形OABC的一组对边OC、AB分别交于点M、N,延长OC、AB交于点D,由条件可以得出AD=6,就可以求出△OAD的面积,再根据问题迁移的结论就可以求出最大值;
当过点P的直线l与四边形OABC的另一组对边CB、OA分别交M、N,延长CB交x轴于T,由B、C的坐标可得直线BC的解析式,就可以求出T的坐标,从而求出△OCT的面积,再由问题迁移的结论可以求出最大值,通过比较就可以求出结论.
(1)证明:![]() ,
,
![]()
![]() 点
点![]() 为
为![]() 边的中点,
边的中点,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
即![]()
(2)当直线旋转到点![]() 是
是![]() 的中点时,
的中点时,![]() 最小,如图2,
最小,如图2,

过点![]() 的另一条直线
的另一条直线![]() 交
交![]() 于点
于点![]() ,
,
设![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于
于![]() ,
,
由问题情境可以得出当![]() 是
是![]() 的中点时.
的中点时.![]()
![]() ,
,
![]() ,
,
![]() 当点
当点![]() 是
是![]() 的中点时,
的中点时,![]() 最小
最小
(3)如图3,作![]() ,垂足分别为
,垂足分别为![]() ,
,
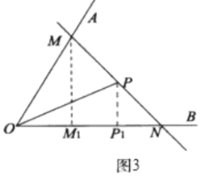
在![]() 中,
中,
![]() ,
,
![]() .
.
由问题迁移的结论知道,
当![]() 时,
时,![]() 的面积最小,
的面积最小,
![]() .
.
在![]() 中,
中,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]()
(4)①如图4,当过点![]() 的直线
的直线![]() 与四边形
与四边形![]() 的一组对边
的一组对边![]() 分别交于点
分别交于点![]() ,延长
,延长![]() 交于点
交于点![]() ,
,
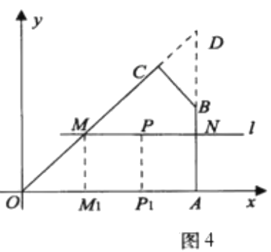
![]()
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
由问题迁移的结论可知,当![]() 时,
时,![]() 的面积最小,
的面积最小,
![]() 四边形
四边形![]() 的面积最大.
的面积最大.
作![]() 垂足分别为
垂足分别为![]() ,
,
![]()
![]() 点
点![]() 为
为![]() 中点
中点
![]() ,
,
![]()
![]()
②如图5,当过点![]() 的直线
的直线![]() 与四边形
与四边形![]() 的另一组对
的另一组对![]() 边分别交
边分别交![]() 延长
延长![]() 交
交![]() 轴于
轴于![]() ,
,

![]() ,
,![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,由题意,得
,由题意,得
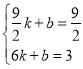 ,解得
,解得![]()
![]() ,
,
当![]() 时,
时,![]() ,
,
![]()
![]()
由问题迁移的结论可知,当![]() 时,
时,![]() 的面积最小,
的面积最小,
![]() 四边形
四边形![]() 的面积最大.
的面积最大.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
综上所述:截得四边形面积的最大值为![]() .
.


科目:初中数学 来源: 题型:
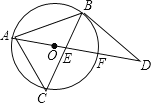
【题目】如图,点O为△ABC外接圆的圆心,以AB为腰作等腰△ABD,使底边AD经过点O,并分别交BC于点E、交⊙O于点F,若∠BAD=30°.
(1)求证:BD是⊙O的切线;
(2)当CA2=CECB时,
①求∠ABC的度数;
②![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市用3400元购进A、B两种文具盒共120个,这两种文具盒的进价、标价如下表:
价格/类型 | A型 | B型 |
进价(元/只) | 15 | 35 |
标价(元/只) | 25 | 50 |
(1)这两种文具盒各购进多少只?
(2)若A型文具盒按标价的9折出售,B型文具盒按标价的8折出售,那么这批文具盒全部售出后,超市共获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在阳光体育活动时间,小亮、小莹、小芳到学校乒乓球室打乒乓球,当时只有一副空球桌,他们只能选两人打第一场.
(1)如果确定小亮打第一场,再从其余两人中随机选取一人打第一场,选中小莹的概率是________.
(2)如果确定小亮打第一场,用投掷硬币的方法确定小莹、小芳谁打第一场,并决定小亮做裁判,由小亮抛掷一枚硬币,规定正面朝上小莹胜,反面朝上小芳胜,最终胜两局以上者(包括两局)打第一场.小亮第一次投掷的结果是正面朝上,请用列表或画树状图的方法表示最后两次投掷硬币的所有情况,并求小芳打第一场的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一平面坐标系中,函数y=mx+m和y=﹣mx2+2x+2(m是常数,且m≠0)的图象可能是( )
A. 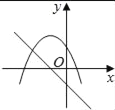 B.
B. 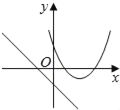 C.
C. 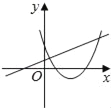 D.
D. 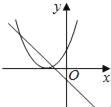
【答案】D
【解析】A.由函数y=mx+m的图象可知m<0,即函数y=mx2+2x+2开口方向朝上,与图象不符,故A选项错误;
B.由函数y=mx+m的图象可知m<0,对称轴为x=![]() <0,则对称轴应在y轴左侧,与图象不符,故B选项错误;
<0,则对称轴应在y轴左侧,与图象不符,故B选项错误;
C.由函数y=mx+m的图象可知m>0,即函数y=mx2+2x+2开口方向朝下,与图象不符,故C选项错误;
D.由函数y=mx+m的图象可知m<0,即函数y=mx2+2x+2开口方向朝上,对称轴为x=![]() <0,则对称轴应在y轴左侧,与图象相符,故D选项正确;
<0,则对称轴应在y轴左侧,与图象相符,故D选项正确;
故选:D.
【题型】单选题
【结束】
10
【题目】如图,已知菱形ABCD的周长为16,面积为![]() ,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为( )
,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为( )
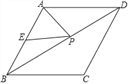
A. 2 B. 2![]() C. 4 D. 4
C. 4 D. 4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() x2+
x2+![]() x+3与x轴交于点A,B(点A在点B的左边),交y轴于点C,点P为抛物线对称轴上一点.则△APC的周长最小值是_____.
x+3与x轴交于点A,B(点A在点B的左边),交y轴于点C,点P为抛物线对称轴上一点.则△APC的周长最小值是_____.
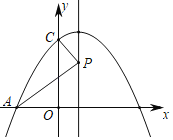
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为5,点A的坐标为(﹣4,0),点B在y轴上,若反比例函数![]() (k≠0)的图象过点C,则该反比例函数的表达式为( )
(k≠0)的图象过点C,则该反比例函数的表达式为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com