
【题目】某超市用3400元购进A、B两种文具盒共120个,这两种文具盒的进价、标价如下表:
价格/类型 | A型 | B型 |
进价(元/只) | 15 | 35 |
标价(元/只) | 25 | 50 |
(1)这两种文具盒各购进多少只?
(2)若A型文具盒按标价的9折出售,B型文具盒按标价的8折出售,那么这批文具盒全部售出后,超市共获利多少元?
科目:初中数学 来源: 题型:
【题目】完成下面推理过程
如图,已知DE∥BC,DF、BE分别平分∠ADE、∠ABC,可推得∠FDE=∠DEB的理由:

∵DE∥BC(已知)
∴∠ADE= .( )
∵DF、BE分别平分∠ADE、∠ABC,
∴∠ADF=![]() ,
,
∠ABE=![]() .( )
.( )
∴∠ADF=∠ABE
∴DF∥ .( )
∴∠FDE=∠DEB. ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
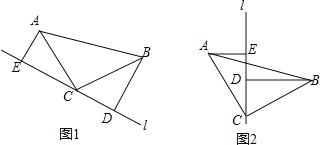
【题目】如图,△ABC中,∠ACB=90°,AC=BC,直线l过点C,BD⊥l,AE⊥l,垂足分别为D、E.
(1)当直线l不与底边AB相交时,求证:ED=AE+BD;
(2)如图2,将直线l绕点C顺时针旋转,使l与底边AB相交时,请你探究ED、AE、BD三者之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在Rt△ABC中,∠C=90°,AB=10,BC=6,点P从点A出发,沿折线AB﹣BC向终点C运动,在AB上以每秒5个单位长度的速度运动,在BC上以每秒3个单位长度的速度运动,点Q从点C出发,沿CA方向以每秒 ![]() 个单位长度的速度运动,P,Q两点同时出发,当点P停止时,点Q也随之停止.设点P运动的时间为t秒.
个单位长度的速度运动,P,Q两点同时出发,当点P停止时,点Q也随之停止.设点P运动的时间为t秒.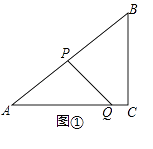
(1)求线段AQ的长;(用含t的代数式表示)
(2)连结PQ,当PQ与△ABC的一边平行时,求t的值;
(3)如图②,过点P作PE⊥AC于点E,以PE,EQ为邻边作矩形PEQF,点D为AC的中点,连结DF.设矩形PEQF与△ABC重叠部分图形的面积为S.①当点Q在线段CD上运动时,求S与t之间的函数关系式;②直接写出DF将矩形PEQF分成两部分的面积比为1:2时t的值.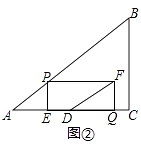
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AB=4,BC=6,∠B=60°,将△ABC沿着射线BC 的方向平移 2 个单位后,得到△△A′B′C′,连接 A′C,则△A′B′C 的周长为__________ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在Rt△ABC中,∠C=90°,沿过B点的一条直线BE折叠这个三角形, 使C点与AB边上的一点D重合.
(1)当∠A满足什么条件时,点D恰为AB的中点?写出一个你认为适当的条件,并利用此条件证明D为AB的中点;
(2)在(1)的条件下,若DE=1,求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
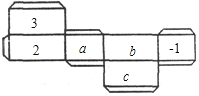
【题目】如图是一个长方体纸盒的平面展开图,已知纸盒中相对两个面上的数互为相反数.
(1)填空:a=______,b=______,c=______.
(2)先化简,再求值:-a2b+2(3ab2-a2b)-3(2ab2-a2b)+abc
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com