
ΓΨΧβΡΩΓΩ»γΆΦΔΌΘ§‘ΎRtΓςABC÷–Θ§ΓœC=90ΓψΘ§AB=10Θ§BC=6Θ§ΒψP¥”ΒψA≥ωΖΔΘ§―Ί’έœΏAB©¹BCœρ÷’ΒψC‘ΥΕ·Θ§‘ΎAB…œ“‘ΟΩΟκ5ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»‘ΥΕ·Θ§‘ΎBC…œ“‘ΟΩΟκ3ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»‘ΥΕ·Θ§ΒψQ¥”ΒψC≥ωΖΔΘ§―ΊCAΖΫœρ“‘ΟΩΟκ ![]() ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»‘ΥΕ·Θ§PΘ§QΝΫΒψΆ§ ±≥ωΖΔΘ§Β±ΒψPΆΘ÷Ι ±Θ§ΒψQ“≤Υφ÷°ΆΘ÷ΙΘ°…ηΒψP‘ΥΕ·ΒΡ ±ΦδΈΣtΟκΘ°
ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»‘ΥΕ·Θ§PΘ§QΝΫΒψΆ§ ±≥ωΖΔΘ§Β±ΒψPΆΘ÷Ι ±Θ§ΒψQ“≤Υφ÷°ΆΘ÷ΙΘ°…ηΒψP‘ΥΕ·ΒΡ ±ΦδΈΣtΟκΘ°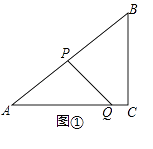
Θ®1Θ©«σœΏΕΈAQΒΡ≥ΛΘΜΘ®”ΟΚ§tΒΡ¥ζ ΐ Ϋ±μ ΨΘ©
Θ®2Θ©Ν§ΫαPQΘ§Β±PQ”κΓςABCΒΡ“Μ±ΏΤΫ–– ±Θ§«σtΒΡ÷ΒΘΜ
Θ®3Θ©»γΆΦΔΎΘ§ΙΐΒψPΉςPEΓΆAC”ΎΒψEΘ§“‘PEΘ§EQΈΣΝΎ±ΏΉςΨΊ–ΈPEQFΘ§ΒψDΈΣACΒΡ÷–ΒψΘ§Ν§ΫαDFΘ°…ηΨΊ–ΈPEQF”κΓςABC÷ΊΒΰ≤ΩΖ÷ΆΦ–ΈΒΡΟφΜΐΈΣSΘ°ΔΌΒ±ΒψQ‘ΎœΏΕΈCD…œ‘ΥΕ· ±Θ§«σS”κt÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘΜΔΎ÷±Ϋ”–¥≥ωDFΫΪΨΊ–ΈPEQFΖ÷≥…ΝΫ≤ΩΖ÷ΒΡΟφΜΐ±»ΈΣ1ΘΚ2 ±tΒΡ÷ΒΘ°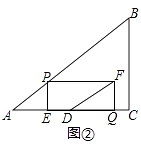
ΓΨ¥πΑΗΓΩ
Θ®1Θ©ΫβΘΚ‘ΎRtΓςABC÷–Θ§ΓΏΓœC=90ΓψΘ§AB=10Θ§BC=6Θ§
ΓύAC= ![]() =
= ![]() =8Θ§
=8Θ§
ÿCQ= ![]() tȧ
tȧ
ΓύAQ=8©¹ ![]() tΘ®0ΓήtΓή4Θ©Θ°
tΘ®0ΓήtΓή4Θ©Θ°
Θ®2Θ©ΫβΘΚΔΌΒ±PQΓΈBC ±Θ§ ![]() =
= ![]() Θ§
Θ§
Γύ ![]() =
= ![]() Θ§
Θ§
Γύt= ![]() sΘ°
sΘ°
ΔΎΒ±PQΓΈAB ±Θ§ ![]() =
= ![]() Θ§
Θ§
Γύ ![]() =
= ![]() Θ§
Θ§
Γύt=3Θ§
Ήέ…œΥυ ωΘ§t= ![]() sΜρ3s ±Θ§Β±PQ”κΓςABCΒΡ“Μ±ΏΤΫ––Θ°
sΜρ3s ±Θ§Β±PQ”κΓςABCΒΡ“Μ±ΏΤΫ––Θ°
Θ®3Θ©ΫβΘΚΔΌ»γΆΦ1÷–Θ§aΓΔΒ±0ΓήtΓή ![]() ±Θ§÷ΊΒΰ≤ΩΖ÷ «ΥΡ±Ώ–ΈPEQFΘ°
±Θ§÷ΊΒΰ≤ΩΖ÷ «ΥΡ±Ώ–ΈPEQFΘ°
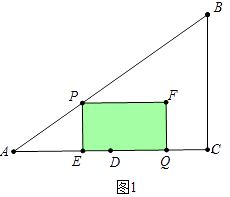
S=PEEQ=3tΘ®8©¹4t©¹ ![]() tΘ©=©¹16t2+24tΘ°
tΘ©=©¹16t2+24tΘ°
bΓΔ»γΆΦ2÷–Θ§Β± ![]() ΘΦtΓή2 ±Θ§÷ΊΒΰ≤ΩΖ÷ «ΥΡ±Ώ–ΈPNQEΘ°
ΘΦtΓή2 ±Θ§÷ΊΒΰ≤ΩΖ÷ «ΥΡ±Ώ–ΈPNQEΘ°
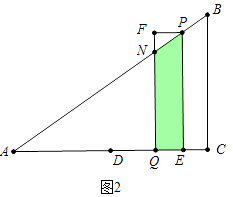
S=SΥΡ±Ώ–ΈPEQF©¹SΓςPFN=Θ®16t2©¹24tΘ©©¹ ![]()
![]() [5t©¹
[5t©¹ ![]() Θ®8©¹
Θ®8©¹ ![]() tΘ©]
tΘ©] ![]() [5t©¹
[5t©¹ ![]()
![]() tΘ©]=
tΘ©]= ![]() Θ°
Θ°
cΓΔ»γΆΦ3÷–Θ§Β±2ΘΦtΓή3 ±Θ§÷ΊΒΰ≤ΩΖ÷ «Έε±Ώ–ΈMNPBQΘ°
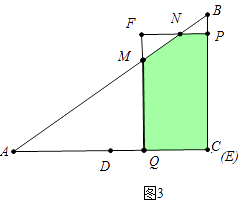
S=SΥΡ±Ώ–ΈPBQF©¹SΓςFNM= ![]() t[6©¹3Θ®t©¹2Θ©]©¹
t[6©¹3Θ®t©¹2Θ©]©¹ ![]() [
[ ![]() t©¹4Θ®t©¹2Θ©]
t©¹4Θ®t©¹2Θ©] ![]() [
[ ![]() t©¹4Θ®t©¹2Θ©]=©¹
t©¹4Θ®t©¹2Θ©]=©¹ ![]() t2+32t©¹24Θ°
t2+32t©¹24Θ°
ΔΎaΓΔ»γΆΦ4÷–Θ§Β±DEΘΚDQ=1ΘΚ2 ±Θ§DFΫΪΨΊ–ΈPEQFΖ÷≥…ΝΫ≤ΩΖ÷ΒΡΟφΜΐ±»ΈΣ1ΘΚ2Θ°
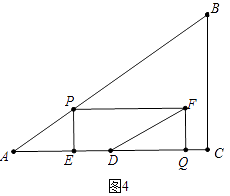
‘ρ”–Θ®4©¹4tΘ©ΘΚΘ®4©¹ ![]() tΘ©=1ΘΚ2Θ§ΫβΒΟt=
tΘ©=1ΘΚ2Θ§ΫβΒΟt= ![]() sΘ§
sȧ
bΓΔ»γΆΦ5÷–Θ§Β±NEΘΚPN=1ΘΚ2 ±Θ§DFΫΪΨΊ–ΈPEQFΖ÷≥…ΝΫ≤ΩΖ÷ΒΡΟφΜΐ±»ΈΣ1ΘΚ2Θ°
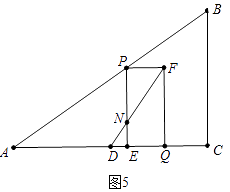
ΓύDEΘΚDQ=NEΘΚFQ=1ΘΚ3Θ§
ΓύΘ®4t©¹4Θ©ΘΚΘ®4©¹ ![]() tΘ©=1ΘΚ3Θ§
tΘ©=1ΘΚ3Θ§
ΫβΒΟt= ![]() sΘ§
sȧ
Ήέ…œΥυ ωΘ§Β±t= ![]() sΜρ
sΜρ ![]() s ±Θ§DFΫΪΨΊ–ΈPEQFΖ÷≥…ΝΫ≤ΩΖ÷ΒΡΟφΜΐ±»ΈΣ1ΘΚ2Θ°
s ±Θ§DFΫΪΨΊ–ΈPEQFΖ÷≥…ΝΫ≤ΩΖ÷ΒΡΟφΜΐ±»ΈΣ1ΘΚ2Θ°
ΓΨΫβΈωΓΩΘ®1Θ©”…œΏΕΈ÷°≤νΩ…±μ Ψ≥ωAQ=8©¹ ![]() t;Θ®2Θ©”…”ΎΒψQ‘ΎAC…œΘ§PQ≤ΜΜα”κACΤΫ––Θ§“ρ¥ΥΖ÷άύΧ÷¬έPQΓΈBC”κPQΓΈABΝΫάύΘΜΘ®2Θ©“‘t=2ΚΆ
t;Θ®2Θ©”…”ΎΒψQ‘ΎAC…œΘ§PQ≤ΜΜα”κACΤΫ––Θ§“ρ¥ΥΖ÷άύΧ÷¬έPQΓΈBC”κPQΓΈABΝΫάύΘΜΘ®2Θ©“‘t=2ΚΆ![]() ΈΣΖ÷ΫγΒψΖ÷ΈΣ»ΐΕΈΘΚ0ΓήtΓή
ΈΣΖ÷ΫγΒψΖ÷ΈΣ»ΐΕΈΘΚ0ΓήtΓή ![]() ΓΔ
ΓΔ ![]() ΘΦtΓή2ΓΔ2ΘΦtΓή3ΘΜΘ®3Θ©–ηΖ÷άύΈΣΝΫ÷÷ΘΚΉσ…œΘΚ”“œ¬=1ΘΚ2ΚΆΉσ…œΘΚ”“œ¬=2ΘΚ1.
ΘΦtΓή2ΓΔ2ΘΦtΓή3ΘΜΘ®3Θ©–ηΖ÷άύΈΣΝΫ÷÷ΘΚΉσ…œΘΚ”“œ¬=1ΘΚ2ΚΆΉσ…œΘΚ”“œ¬=2ΘΚ1.
ΓΨΩΦΒψΨΪΈωΓΩΙΊ”Ύ±ΨΧβΩΦ≤ιΒΡΚ· ΐΙΊœΒ ΫΘ§–η“ΣΝΥΫβ”Οά¥±μ ΨΚ· ΐΙΊœΒΒΡ ΐ―ß ΫΉ”Ϋ–ΉωΚ· ΐΫβΈω ΫΜρΚ· ΐΙΊœΒ Ϋ≤≈ΡήΒΟ≥ω’ΐ»Ζ¥πΑΗΘ°


 ABCΩΦΆθ»Ϊ”≈ΨμœΒΝ–¥πΑΗ
ABCΩΦΆθ»Ϊ”≈ΨμœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΥΒΟςάμ”…
»γΆΦΘ§Γœ1ΘΪΓœ2ΘΫ230ΓψΘ§bΓΈcΘ§ ‘ρΓœ1ΓΔΓœ2ΓΔΓœ3ΓΔΓœ4Ης «Εύ…ΌΕ»ΘΩ

ΫβΘΚΓΏ Γœ1ΘΫΓœ2 (_________________________)
Γœ1ΘΪΓœ2ΘΫ230Γψ
ΓύΓœ1 ΘΫΓœ2 ΘΫ________Θ®ΧνΕ» ΐΘ©
ΓΏ bΓΈc
ΓύΓœ4 ΘΫΓœ2ΘΫ ________Θ®ΧνΕ» ΐΘ©
( )
Γœ2 ΘΪΓœ3 ΘΫ180Γψ ( )
ΓύΓœ3 ΘΫ180ΓψΘ≠Γœ2 ΘΫ_________Θ®ΧνΕ» ΐΘ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“ΜΗω≤ΜΆΗΟςΒΡΩΎ¥ϋ÷–”–“ΜΗω–Γ«ρΘ§…œΟφΖ÷±π±ξ”–Ή÷ΡΗaΘ§bΘ§cΘ§ΟΩΗω–Γ«ρ≥ΐΉ÷ΡΗ≤ΜΆ§ΆβΤδ”ύΨυœύΆ§Θ§–Γ‘ΑΆ§―ߥ”ΩΎ¥ϋ÷–ΥφΜζΟΰ≥ω“ΜΗω–Γ«ρΘ§Φ«œ¬Ή÷ΡΗΚσΖ≈ΜΊ«“ΫΝ‘»Θ§‘Ό¥”Ω…ΩΎ¥ϋ÷–ΥφΜζΟΰ≥ω“ΜΗω–Γ«ρΦ«œ¬Ή÷ΡΗΘ°”ΟΜ≠ ςΉ¥ΆΦΘ®ΜρΝ–±μΘ©ΒΡΖΫΖ®Θ§«σ–Γ‘ΑΆ§―ßΝΫ¥ΈΟΰ≥ωΒΡ–Γ«ρ…œΒΡΉ÷ΡΗœύΆ§ΒΡΗ≈¬ Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΝΫΗυΡΨΧθΘ§“ΜΗυ≥Λ20cmΘ§Νμ“ΜΗυ≥Λ24cmΘ§ΫΪΥϋΟ«“ΜΕΥ÷ΊΚœ«“Ζ≈‘ΎΆ§“ΜΧθ÷±œΏ…œΘ§¥Υ ±ΝΫΗυΡΨΧθΒΡ÷–Βψ÷°ΦδΒΡΨύάκΈΣ(ΓΓΓΓ)
A. 2cm B. 4cm C. 2cmΜρ22cm D. 4cmΜρ44cm
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΦΉΓΔ““ΝΫ≥ΒΦδΆ§ ±ΩΣ ΦΦ”ΙΛ“Μ≈ζΖΰΉΑΘ°¥”ΩΣ ΦΦ”ΙΛΒΫΦ”ΙΛΆξ’β≈ζΖΰΉΑΦΉ≥ΒΦδΙΛΉςΝΥ9–Γ ±Θ§““≥ΒΦδ‘Ύ÷–ΆΨΆΘΙΛ“ΜΕΈ ±ΦδΈ§–ό…η±ΗΘ§»ΜΚσΑ¥ΆΘΙΛ«ΑΒΡΙΛΉς–߬ ΦΧ–χΦ”ΙΛΘ§÷±ΒΫ”κΦΉ≥ΒΦδΆ§ ±Άξ≥…’β≈ζΖΰΉΑΒΡΦ”ΙΛ»ΈΈώΈΣ÷ΙΘ°…ηΦΉΓΔ““ΝΫ≥ΒΦδΗςΉ‘Φ”ΙΛΖΰΉΑΒΡ ΐΝΩΈΣyΘ®ΦΰΘ©Θ°ΦΉ≥ΒΦδΦ”ΙΛΒΡ ±ΦδΈΣxΘ® ±Θ©Θ§y”κx÷°ΦδΒΡΚ· ΐΆΦœσ»γΆΦΥυ ΨΘ°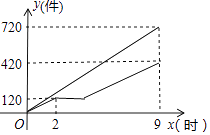
Θ®1Θ©ΦΉ≥ΒΦδΟΩ–Γ ±Φ”ΙΛΖΰΉΑΦΰ ΐΈΣΦΰΘΜ’β≈ζΖΰΉΑΒΡΉήΦΰ ΐΈΣΦΰΘ°
Θ®2Θ©«σ““≥ΒΦδΈ§–ό…η±ΗΚσΘ§““≥ΒΦδΦ”ΙΛΖΰΉΑ ΐΝΩy”κx÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘΜ
Θ®3Θ©«σΦΉΓΔ““ΝΫ≥ΒΦδΙ≤Ά§Φ”ΙΛΆξ1000ΦΰΖΰΉΑ ±ΦΉ≥ΒΦδΥυ”ΟΒΡ ±ΦδΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥≥§ –”Ο3400‘ΣΙΚΫχAΓΔBΝΫ÷÷ΈΡΨΏΚ–Ι≤120ΗωΘ§’βΝΫ÷÷ΈΡΨΏΚ–ΒΡΫχΦέΓΔ±ξΦέ»γœ¬±μΘΚ
ΦέΗώ/άύ–Ά | A–Ά | B–Ά |
ΫχΦέΘ®‘Σ/÷ΜΘ© | 15 | 35 |
±ξΦέΘ®‘Σ/÷ΜΘ© | 25 | 50 |
Θ®1Θ©’βΝΫ÷÷ΈΡΨΏΚ–ΗςΙΚΫχΕύ…Ό÷ΜΘΩ
Θ®2Θ©»τA–ΆΈΡΨΏΚ–Α¥±ξΦέΒΡ9’έ≥ω έΘ§B–ΆΈΡΨΏΚ–Α¥±ξΦέΒΡ8’έ≥ω έΘ§Ρ«Ο¥’β≈ζΈΡΨΏΚ–»Ϊ≤Ω έ≥ωΚσΘ§≥§ –Ι≤ΜώάϊΕύ…Ό‘ΣΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΘΚ»γΆΦΘ§‘ΎRtΓςABC÷–Θ§ΓœACBΘΫ90ΓψΘ§ACΘΫBCΘ§ΒψD «BCΒΡ÷–ΒψΘ§CEΓΆADΘ§¥ΙΉψΈΣΒψEΘ§BFΓΈACΫΜCEΒΡ―”≥ΛœΏ”ΎΒψFΘ°
«σ÷ΛΘΚACΘΫ2BFΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ–ΓΚλ≤Μ–Γ–ΡΑ―Φ“άοΒΡ“ΜΩι‘≤–Έ≤ΘΝߥρΥιΝΥΘ§–η“Σ≈δ÷Τ“ΜΩιΆ§―υ¥σ–ΓΒΡ≤ΘΝßΨΒΘ§ΙΛ»Υ ΠΗΒ‘Ύ“ΜΩι»γΆΦΥυ ΨΒΡ≤ΘΝßΨΒ≤–Τ§ΒΡ±Ώ‘ΒΟη≥ωΝΥΒψAΘ§BΘ§CΘ§Ηχ≥ω»ΐΫ«–ΈABCΘ§‘ρ’βΩι≤ΘΝßΨΒΒΡ‘≤–Ρ «Θ® Θ©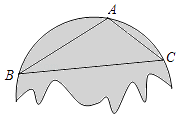
A.ABΘ§AC±Ώ…œΒΡ÷–œΏΒΡΫΜΒψ
B.ABΘ§AC±Ώ…œΒΡ¥Ι÷±ΤΫΖ÷œΏΒΡΫΜΒψ
C.ABΘ§AC±Ώ…œΒΡΗΏΥυ‘Ύ÷±œΏΒΡΫΜΒψ
D.ΓœBAC”κΓœABCΒΡΫ«ΤΫΖ÷œΏΒΡΫΜΒψ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com