
【题目】小红不小心把家里的一块圆形玻璃打碎了,需要配制一块同样大小的玻璃镜,工人师傅在一块如图所示的玻璃镜残片的边缘描出了点A,B,C,给出三角形ABC,则这块玻璃镜的圆心是( )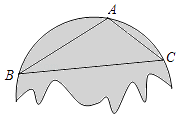
A.AB,AC边上的中线的交点
B.AB,AC边上的垂直平分线的交点
C.AB,AC边上的高所在直线的交点
D.∠BAC与∠ABC的角平分线的交点
科目:初中数学 来源: 题型:
【题目】将两个大小不同的含30°角的三角板的直角顶点O重合在一起,保持△COD不动,将△AOB绕点O旋转,设射线AB与射线DC交于点F.
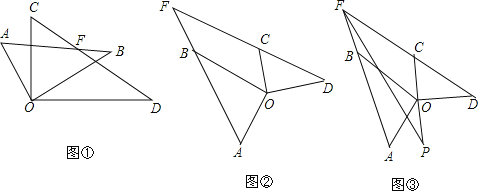
(1)如图①,若∠AOD=120°,
①AB与OD的位置关系 .
②∠AFC的度数= .
(2)如图②当∠AOD=130°,求∠AFC的度数.
(3)由上述结果,写出∠AOD和∠AFC的关系 .
(4)如图③,作∠AFC、∠AOD的角平分线交于点P,求∠P的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在Rt△ABC中,∠C=90°,AB=10,BC=6,点P从点A出发,沿折线AB﹣BC向终点C运动,在AB上以每秒5个单位长度的速度运动,在BC上以每秒3个单位长度的速度运动,点Q从点C出发,沿CA方向以每秒 ![]() 个单位长度的速度运动,P,Q两点同时出发,当点P停止时,点Q也随之停止.设点P运动的时间为t秒.
个单位长度的速度运动,P,Q两点同时出发,当点P停止时,点Q也随之停止.设点P运动的时间为t秒.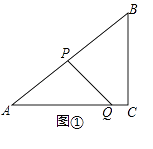
(1)求线段AQ的长;(用含t的代数式表示)
(2)连结PQ,当PQ与△ABC的一边平行时,求t的值;
(3)如图②,过点P作PE⊥AC于点E,以PE,EQ为邻边作矩形PEQF,点D为AC的中点,连结DF.设矩形PEQF与△ABC重叠部分图形的面积为S.①当点Q在线段CD上运动时,求S与t之间的函数关系式;②直接写出DF将矩形PEQF分成两部分的面积比为1:2时t的值.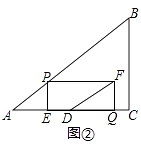
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在Rt△ABC中,∠C=90°,沿过B点的一条直线BE折叠这个三角形, 使C点与AB边上的一点D重合.
(1)当∠A满足什么条件时,点D恰为AB的中点?写出一个你认为适当的条件,并利用此条件证明D为AB的中点;
(2)在(1)的条件下,若DE=1,求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=30,C为射线AB上一点,BC比AC的4倍少20,P,Q两点分别从A,B两点同时出发.分别以2单位/秒和1单位/秒的速度在射线AB上沿AB方向运动,运动时间为t秒,M为BP的中点,N为QM的中点,以下结论:①BC=2AC;②运动过程中,QM的长度保持不变;③AB=4NQ;④当BQ=PB时,t=12,其中正确结论的个数是( )

A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织了一次防溺水、防交通事故、防食物中毒、防校园欺凌及其他各种安全意识的调查活动,了解同学们在哪些方面的安全意识薄弱,便于今后更好地开展安全教育活动.根据调查结果,绘制出图1,图2两幅不完整的统计图.
请结合图中的信息解答下列问题: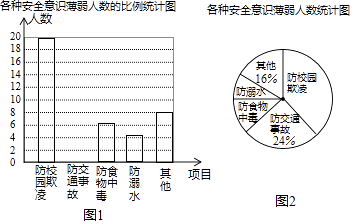
(1)本次调查的人数为 , 其中防校园欺凌意识薄弱的人数占%;
(2)补全条形统计图;
(3)若该校共有1500名学生,请估计该校学生中防溺水意识薄弱的人数;
(4)请你根据题中的信息,给该校的安全教育提一个合理的建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书店老板去图书批发市场购买某种图书,第一次用1200元购书若干本,并按该书定价7元出售,很快售完.由于该书畅销,第二次购书时,每本书的批发价已比第一次提高了20%,他用1500元所购该书的数量比第一次多10本,当按定价售出200本时,出现滞销,便以定价的4折售完剩余的书.
(1)第一次购书的进价是多少元?
(2)试问该老板这两次售书总体上是赔钱了,还是赚钱了(不考虑其他因素)?若赔钱,赔多少;若赚钱,赚多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学“综合与实践”课中,老师带领同学们来到娄底市郊区,测算如图所示的仙女峰的高度,李红盛同学利用已学的数学知识设计了一个实践方案,并实施了如下操作:先在水平地面A处测得山顶B的仰角∠BAC为38.7°,再由A沿水平方向前进377米到达山脚C处,测得山坡BC的坡度为1:0.6,请你求出仙女峰的高度(参考数据:tan38.7°≈0.8)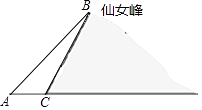
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com