【题目】数学“综合与实践”课中，老师带领同学们来到娄底市郊区，测算如图所示的仙女峰的高度，李红盛同学利用已学的数学知识设计了一个实践方案，并实施了如下操作：先在水平地面A处测得山顶B的仰角∠BAC为38.7°，再由A沿水平方向前进377米到达山脚C处，测得山坡BC的坡度为1：0.6，请你求出仙女峰的高度（参考数据：tan38.7°≈0.8）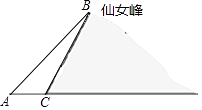
【答案】解：如图，过点B作BD⊥AC于点D，
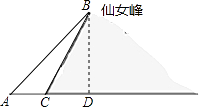
∵山坡BC的坡度为1：0.6，
∴ 
= 
，
则CD=0.6BD．
∵∠BAC为38.7°，
∴tan38.7°= 
= 
．
∵AC=377米，tan38.7°≈0.8，
∴ 
≈0.8，
解得BD=725（米）．
答：仙女峰的高度约为725米．
【解析】图中有两个直角三角形
BCD和ABD，先由坡度的定义：坡度=铅垂高度
水平距离，得出CD、BD的关系，在ABD中利用tan38.7°=
列出方程，求出BD.
【考点精析】关于本题考查的关于坡度坡角问题，需要了解坡面的铅直高度h和水平宽度l的比叫做坡度(坡比)．用字母i表示，即i=h/l．把坡面与水平面的夹角记作A(叫做坡角)，那么i=h/l=tanA才能得出正确答案．
课时训练江苏人民出版社系列答案科目：初中数学 来源： 题型：
【题目】小红不小心把家里的一块圆形玻璃打碎了，需要配制一块同样大小的玻璃镜，工人师傅在一块如图所示的玻璃镜残片的边缘描出了点A，B，C，给出三角形ABC，则这块玻璃镜的圆心是（ ）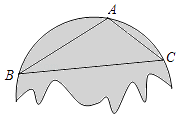
A.AB，AC边上的中线的交点
B.AB，AC边上的垂直平分线的交点
C.AB，AC边上的高所在直线的交点
D.∠BAC与∠ABC的角平分线的交点
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了解我市的空气质量情况，某环保兴趣小组从环境监测网随机抽取了若干天的空气质量情况作为样本进行统计，绘制了如图所示的条形统计图和扇形统计图（部分信息未给出）．
请你根据图中提供的信息，解答下列问题：
（1）请补全条形统计图，并求扇形统计图中表示“重度污染”的扇形的圆心角度数；
（2）所抽取若干天的空气质量情况的众数是 中位数是 ．
（3）请估计该市这一年（365天）达到“优”和“良”的总天数．
查看答案和解析>>
科目：初中数学 来源： 题型：
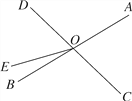
【题目】如图，直线AB、CD相交于点O，OE把∠BOD分成两部分．
(1)图中∠AOC的对顶角为________，∠BOE的补角为________；
(2)若∠AOC＝75°，且∠BOE∶∠EOD＝1∶4，求∠AOE的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】坐火车从上海到娄底，高铁G1329次列车比快车K575次列车少要9小时，已知上海到娄底的铁路长约1260千米，G1329的平均速度是K575的2.5倍．
（1）求K575的平均速度；
（2）高铁G1329从上海到娄底只需几小时？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB∥CD∥EF，BC∥AD，AC平分∠BAD，且与EF交于点O，那么与∠AOE相等的角有（ ）
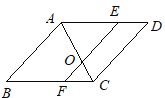
A. 6个B. 5个C. 4个D. 3个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】[知识生成]通常，用两种不同的方法计算同一个图形的面积，可以得到一个恒等式.例如：如图①是一个长为
，宽为
的长方形，沿图中虚线用剪刀均分成四个小长方形，然后按图②的形状拼成一个正方形．请解答下列问题：
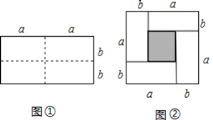
（1）图②中阴影部分的正方形的边长是________________;
（2）请用两种不同的方法求图②中阴影部分的面积：
方法1:________________________；方法2：_______________________;
（3）观察图②，请你写出
、
、
之间的等量关系是__________;
（4）根据（3）中的等量关系解决如下问题：若
,
,则
=________;
[知识迁移]
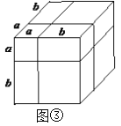
类似地，用两种不同的方法计算同一几何体的体积，也可以得到一个恒等式.
（5）根据图③，写出一个代数恒等式：____________________________;
（6）已知
，
，利用上面的规律求
的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知一次函数y=2x+4
（1）在如图所示的平面直角坐标系中，画出函数的图象；
2）求图象与x轴的交点A的坐标，与y轴交点B的坐标；
（3）在（2）的条件下，求出△AOB的面积；
（4）利用图象直接写出：当y＜0时，x的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com