
����Ŀ����������С��ͬ�ĺ�30���ǵ����ǰ��ֱ�Ƕ���O�غ���һ�𣬱�����COD����������AOB�Ƶ�O��ת��������AB������DC���ڵ�F��
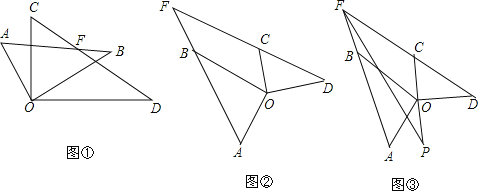
��1����ͼ�٣�����AOD=120�㣬
��AB��OD��λ�ù�ϵ ��
�ڡ�AFC�Ķ���= ��
��2����ͼ�ڵ���AOD=130�������AFC�Ķ�����
��3�������������д����AOD�͡�AFC�Ĺ�ϵ ��
��4����ͼ�ۣ�����AFC����AOD�Ľ�ƽ���߽��ڵ�P�����P�Ķ�����
���𰸡�(1)��AB��OD����30�㣻��2��40�㣻��3����AOD=��AFC+90������4��15��.
��������
��1�����������BOD=30�����Ӷ��õ���B=��BOD���ٸ����ڴ�����ȣ���ֱ��ƽ�н��
�ڸ�����ֱ��ƽ�У�ͬλ����Ƚ�ɣ�
��2�������ܽ������BOC�������ڲ��������OBF�͡�OCF��Ȼ������ı��ε��ڽǺͶ�����ʽ���㼴�ɵý⣻
��3�����ݼ���Ķ���д����ϵʽ���ɣ�
��4����OB��PF�ཻ��G��Ȼ����������ε��ڽǺͶ�����ʽ�������ɵý⣮
��1���١ߡ�AOD=120�㣬
���BOD=��AOD-��AOB=120��-90��=30�㣻
���B=��BOD��
��AB��OD��
�ڡ�AB��OD��
���AFC=��D=30�㣻
��2���ߡ�AOD=130�㣬
���BOC=360��-130��-90���2=50�㣬
�֡ߡ�OBF=180��-30��=150�㣬��OCF=180��-60��=120�㣬
���AFC=360��-150��-120��-50��=40�㣻
��3����AOD=��AFC+90�㣻
��4����OB��PF�ཻ��G��
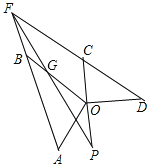
�ߡ�AFC����AOD�Ľ�ƽ���߽��ڵ�P��
���BFG=![]() ��AFC����AOP=
��AFC����AOP=![]() ��AOD��
��AOD��
����BFG����OGP����BFG+��OBF=��POG+��P��
��![]() ��AFC+150��=
��AFC+150��=![]() ��AOD+90��+��P��
��AOD+90��+��P��
��![]() ��AFC+150��=
��AFC+150��=![]() ����AFC+90�㣩+90��+��P��
����AFC+90�㣩+90��+��P��
�����ã���P=15�㣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ��������ABC����ֱ��m�ԳƵġ�A��B��C�䣬��д��A�䡢B�䡢C����������꣨2�����룺����ƽ���������P��x��y������ֱ��m�ԳƵ�P�������Ϊ�� ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��˵������
��ͼ����1����2��230�㣬b��c�� ���1����2����3����4���Ƕ��ٶȣ�

�⣺�� ��1����2 (_________________________)
��1����2��230��
���1 ����2 ��________���������
�� b��c
���4 ����2�� ________���������
( )
��2 ����3 ��180�� ( )
���3 ��180�㣭��2 ��_________���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A1B1C1�У�A1B1��4��A1C1��5��B1C1��7.��A2��B2��C2�ֱ��DZ�B1C1��A1C1��A1B1���е㣻��A3��B3��C3�ֱ��DZ�B2C2��A2C2��A2B2���е㣻�����Դ����ƣ�����A4B4C4���ܳ���________����AnBnCn���ܳ���________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ͼ�������ʡ���չѧϰƬ��չʾ��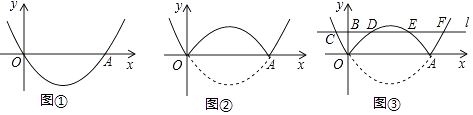
��1�������⡿��ͼ�٣���ƽ��ֱ������ϵ�У�������y=a��x��2��2�� ![]() ����ԭ��O����x�����һ������ΪA����a= ��
����ԭ��O����x�����һ������ΪA����a= ��
��2������������ͼ������������x���·��IJ�����x���۵���x���Ϸ������ⲿ��ͼ����ԭ������ʣ�ಿ�ֵ�ͼ����ɵ���ͼ���ΪG����ͼ�ڣ�ֱ��д��ͼ��G��Ӧ�ĺ�������ʽ��
��3����̽������ͼ���У�����B��0��1����ֱ��lƽ����x�ᣬ��ͼ��G�Ľ��������������Ϊ��C��D��E��F����ͼ�ۣ���ͼ��G��ֱ��l�Ϸ��IJ��ֶ�Ӧ�ĺ���y��x���������ʱx��ȡֵ��Χ��
��4����Ӧ�á�P��ͼ����ͼ��G��һ�㣬�������Ϊm������PD��PE��ֱ��д����PDE�������С��1ʱm��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ʽ��x2+mx��![]() y+3������3x��2y+1��nx2����
y+3������3x��2y+1��nx2����
��1��������ʽ��ֵ����ĸx��ȡֵ�أ���m��n��ֵ��
��2���Ȼ������ʽ3��m2��mn��n2������3m2+mn+n2������������ֵ��
��3���ڣ�1���������£���n+m2��+��2n+![]() m2��+��3n+
m2��+��3n+![]() m2��+��+��9n+
m2��+��+��9n+![]() m2����
m2����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������Ŀڴ�����һ��С������ֱ������ĸa��b��c��ÿ��С�����ĸ��ͬ���������ͬ��Сͬѧ�ӿڴ����������һ��С������ĸ��Ż��ҽ��ȣ��ٴӿɿڴ����������һ��С�������ĸ���û���״ͼ�����б����ķ�������Сͬѧ����������С���ϵ���ĸ��ͬ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ľ����һ����20cm����һ����24cm��������һ���غ��ҷ���ͬһ��ֱ���ϣ���ʱ����ľ�����е�֮��ľ���Ϊ(����)
A. 2cm B. 4cm C. 2cm��22cm D. 4cm��44cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�첻С�İѼ����һ��Բ�β��������ˣ���Ҫ����һ��ͬ����С�IJ�����������ʦ����һ����ͼ��ʾ�IJ�������Ƭ�ı�Ե����˵�A��B��C������������ABC������鲣������Բ���ǣ� ��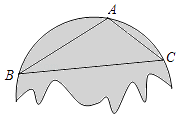
A.AB��AC���ϵ����ߵĽ���
B.AB��AC���ϵĴ�ֱƽ���ߵĽ���
C.AB��AC���ϵĸ�����ֱ�ߵĽ���
D.��BAC���ABC�Ľ�ƽ���ߵĽ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com