
【题目】已知多项式(x2+mx﹣![]() y+3)﹣(3x﹣2y+1﹣nx2).
y+3)﹣(3x﹣2y+1﹣nx2).
(1)若多项式的值与字母x的取值无关,求m,n的值;
(2)先化简多项式3(m2﹣mn﹣n2)﹣(3m2+mn+n2),再求它的值;
(3)在(1)的条件下,求(n+m2)+(2n+![]() m2)+(3n+
m2)+(3n+![]() m2)+…+(9n+
m2)+…+(9n+![]() m2).
m2).
【答案】(1)m=3,n=﹣1(2)8(3)-28
【解析】
(1)先化简代数式,再根据多项式的值与字母x的取值无关,即可得到含x项的系数等于0,即可得出m,n的值;
(2)化简多项式,再把m=3,n=﹣1代入计算即可;
(3)先运用拆项法化简代数式,再把m=3,n=﹣1代入计算即可得到代数式的值.
解:(1)∵(x2+mx﹣![]() y+3)﹣(3x﹣2y+1﹣nx2)
y+3)﹣(3x﹣2y+1﹣nx2)
=(1+n)x2+(m﹣3)x+![]() y+2,
y+2,
∴当多项式的值与字母x的取值无关时,1+n=0,m﹣3=0,
∴m=3,n=﹣1;
(2)3(m2﹣mn﹣n2)﹣(3m2+mn+n2)
=3m2﹣3mn﹣3n2﹣3m2﹣mn﹣n2
=﹣4mn﹣4n2,
当m=3,n=﹣1时,原式=﹣4×(﹣3)﹣4×1=8;
(3)(n+m2)+(2n+![]() m2)+(3n+
m2)+(3n+![]() m2)+…+(9n+
m2)+…+(9n+![]() m2)
m2)
=n+2n+3n+…+9n+m2+![]() m2+
m2+![]() m2+…+
m2+…+![]() m2
m2
=![]() +m2+m2﹣
+m2+m2﹣![]() m2+
m2+![]() m2﹣
m2﹣![]() m2+…+
m2+…+![]() m2﹣
m2﹣![]() m2
m2
=45n+2m2﹣![]() m2
m2
=45n+![]() m2
m2
当m=3,n=﹣1时,原式=﹣45+![]() ×9=﹣45+17=﹣28.
×9=﹣45+17=﹣28.
故答案为:(1)m=3,n=﹣1;(2)8;(3)-28.


科目:初中数学 来源: 题型:
【题目】(1)平面内将一副三角板按如图1所示摆放,∠EBC= °;
(2)平面内将一副三角板按如图2所示摆放,若∠EBC=165°,那么∠α= °;
(3)平面内将一副三角板按如图3所示摆放,∠EBC=115°,求∠α的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面推理过程
如图,已知DE∥BC,DF、BE分别平分∠ADE、∠ABC,可推得∠FDE=∠DEB的理由:

∵DE∥BC(已知)
∴∠ADE= .( )
∵DF、BE分别平分∠ADE、∠ABC,
∴∠ADF=![]() ,
,
∠ABE=![]() .( )
.( )
∴∠ADF=∠ABE
∴DF∥ .( )
∴∠FDE=∠DEB. ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步普及我市中小学生的法律知识,提升学生法律意识,在2018年12月4日第五个国家宪法日来临之际,我市某区在中小学举行了“学习宪法”知识竞赛活动,各类获奖学生人数的比例情况如图所示,其中获得优胜奖的学生共400名,请结合图中信息,解答下列问题:
(1)求获得一等奖的学生人数;
(2)在本次知识竞赛活动中,A,B,C,D四所学校表现突出,现决定从这四所学校中随机选取两所学校举行一场法律知识抢答赛,请用画树状图或列表的方法求恰好选到A,B两所学校的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将两个大小不同的含30°角的三角板的直角顶点O重合在一起,保持△COD不动,将△AOB绕点O旋转,设射线AB与射线DC交于点F.
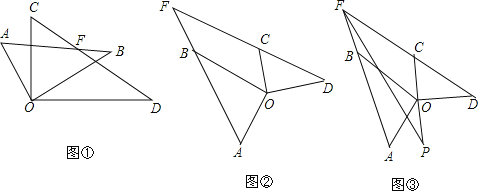
(1)如图①,若∠AOD=120°,
①AB与OD的位置关系 .
②∠AFC的度数= .
(2)如图②当∠AOD=130°,求∠AFC的度数.
(3)由上述结果,写出∠AOD和∠AFC的关系 .
(4)如图③,作∠AFC、∠AOD的角平分线交于点P,求∠P的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(2x-5)(3x+2); (2)(2a+3b)(2a-3b)-(a-3b)2;
(3) (![]() ÷(-3xy); (4)(a+b-c)(a+b+c).
÷(-3xy); (4)(a+b-c)(a+b+c).
查看答案和解析>>
科目:初中数学 来源: 题型:
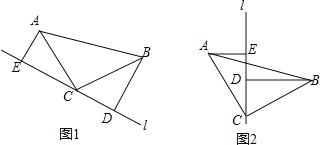
【题目】如图,△ABC中,∠ACB=90°,AC=BC,直线l过点C,BD⊥l,AE⊥l,垂足分别为D、E.
(1)当直线l不与底边AB相交时,求证:ED=AE+BD;
(2)如图2,将直线l绕点C顺时针旋转,使l与底边AB相交时,请你探究ED、AE、BD三者之间的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com