
【题目】如图,△ACB和△ECD都是等腰直角三角形,△ACB的顶点A在△ECD的斜边DE上,
求证: ![]()

【答案】证明见解析.
【解析】试题连结BD,根据等边三角形的性质就可以得出△AEC≌△BDC,就可以得出AE=BD,∠E=∠BDC,由等腰直角三角形的性质就可以得出∠ADB=90°,由勾股定理就可以得出结论.
试题解析:证明:连结BD,
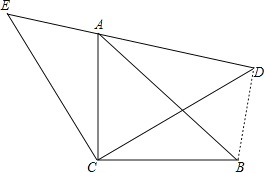
∵△ACB与△ECD都是等腰直角三角形,
∴∠ECD=∠ACB=90°,∠E=∠ADC=∠CAB=45°,
EC=DC,AC=BC,AC2+BC2=AB2,
∴2AC2=AB2.∠ECD-ACD=∠ACB-∠ACD,
∴∠ACE=∠BCD.
在△AEC和△BDC中,
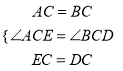 ,
,
∴△AEC≌△BDC(SAS).
∴AE=BD,∠E=∠BDC.
∴∠BDC=45°,
∴∠BDC+∠ADC=90°,
即∠ADB=90°.
∴AD2+BD2=AB2,
∴AD2+AE2=2AC2.


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:初中数学 来源: 题型:
【题目】如图,C为线段AE上一动点(不与A、E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,以下五个结论:①AD=BE;②PQ∥AE;③CP=CQ;④BO=OE;⑤∠AOB=60°,恒成立的结论有

A. ①③⑤ B. ①③④⑤ C. ①②③⑤ D. ①②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△A1B1C1中,A1B1=4,A1C1=5,B1C1=7.点A2,B2,C2分别是边B1C1,A1C1,A1B1的中点;点A3,B3,C3分别是边B2C2,A2C2,A2B2的中点;…;以此类推,则△A4B4C4的周长是________,△AnBnCn的周长是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知多项式(x2+mx﹣![]() y+3)﹣(3x﹣2y+1﹣nx2).
y+3)﹣(3x﹣2y+1﹣nx2).
(1)若多项式的值与字母x的取值无关,求m,n的值;
(2)先化简多项式3(m2﹣mn﹣n2)﹣(3m2+mn+n2),再求它的值;
(3)在(1)的条件下,求(n+m2)+(2n+![]() m2)+(3n+
m2)+(3n+![]() m2)+…+(9n+
m2)+…+(9n+![]() m2).
m2).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中有一个小球,上面分别标有字母a,b,c,每个小球除字母不同外其余均相同,小园同学从口袋中随机摸出一个小球,记下字母后放回且搅匀,再从可口袋中随机摸出一个小球记下字母.用画树状图(或列表)的方法,求小园同学两次摸出的小球上的字母相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
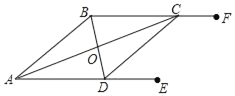
【题目】如图,AE∥BF,AC平分∠BAD,且交BF于点C,BD平分∠ABC,且交AE于点D,连接CD,求证:
(1)AC⊥BD;
(2)四边形ABCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两根木条,一根长20cm,另一根长24cm,将它们一端重合且放在同一条直线上,此时两根木条的中点之间的距离为( )
A. 2cm B. 4cm C. 2cm或22cm D. 4cm或44cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市用3400元购进A、B两种文具盒共120个,这两种文具盒的进价、标价如下表:
价格/类型 | A型 | B型 |
进价(元/只) | 15 | 35 |
标价(元/只) | 25 | 50 |
(1)这两种文具盒各购进多少只?
(2)若A型文具盒按标价的9折出售,B型文具盒按标价的8折出售,那么这批文具盒全部售出后,超市共获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是BC的中点,点E是AD上任意一点.
(1)如图1,连接BE、CE,问:BE=CE成立吗?并说明理由;
(2)如图2,若∠BAC=45°,BE的延长线与AC垂直相交于点F时,问:EF=CF成立吗?并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com