
【题目】已知二次函数y=x2+2x﹣3.
(1)把函数配成y=a(x﹣h)2+k的形式;
(2)求函数与x轴交点坐标;
(3)用五点法画函数图象
x | … | … | |||||
y | … | … |
(4)当y>0时,则x的取值范围为_____.
(5)当﹣3<x<0时,则y的取值范围为_____.

【答案】(1)y=(x+1)2﹣4.
(2) (﹣3,0)和(1,0)
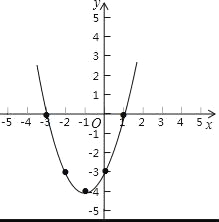
(3) 
(4) x<﹣3或x>1.
(5) ﹣4≤y<0.
【解析】
(1)直接化简函数解析式即可得到所求(2)令y=0就出x的值即可得到结果(3)先作表格,找出对应点的坐标,再根据坐标画出描点连线画出函数图像(4)根据已知条件,结合函数图像即可解答(5)在给定的范围内取值,带入函数中求解即可得到答案.
解:(1)y=x2+2x﹣3=(x+1)2﹣4.
(2)当y=0时,有x2+2x﹣3=0,
解得:x1=﹣3,x2=1,
∴函数y=x2+2x﹣3的图象与x轴交点坐标为(﹣3,0)和(1,0).
(3)当x=﹣3时,y=0;当x=﹣2时,y=﹣3;当x=﹣1时,y=﹣4;当x=0时,y=﹣3;当x=1时,y=0.

用五点法画函数图象.
(4)结合函数图象可知:当x<﹣3 或 x>1时,y>0.
故答案为:x<﹣3或x>1.
(5)当x=﹣1时,y取最小值﹣4;
当x=﹣3时,y=0;
当x=0时,y=﹣3.
∴当﹣3<x<0时,y的取值范围为﹣4≤y<0.



科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+2x+c经过点A(0,3),B(-1,0),请回答下列问题:
(1)求抛物线对应的二次函数的表达式;
(2)抛物线的顶点为D,对称轴与x轴交于点E,连接BD,求BD的长.
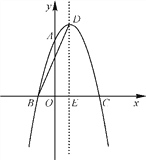
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,M为BC上一点,ME⊥AM,ME交AD的延长线于点E.

(1)求证:△ABM ∽△EMA;
(2)若AB=2,BM=1,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:△PCD是等腰直角三角形,∠DPC=90°,∠APB=135°
求证:(1)△PAC∽△BPD;
(2)若AC=3,BD=1,求CD的长.
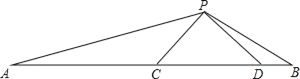
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.
(1)在图1中证明CE=CF;
(2)若∠ABC=90°,G是EF的中点(如图2),直接写出∠BDG的度数;
(3)若∠ABC=120°,FG∥CE,FG=CE,分别连接DB、DG(如图3),求∠BDG的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=-x2+mx+n与x轴交于点A,B(A在B的左侧).
(1)抛物线的对称轴为直线x=-3,AB=4.求抛物线的表达式;
(2)平移(1)中的抛物线,使平移后的抛物线经过点O,且与x正半轴交于点C,记平移后的抛物线顶点为P,若△OCP是等腰直角三角形,求点P的坐标;
(3)当m=4时,抛物线上有两点M(x1,y1)和N(x2,y2),若x1<2,x2>2,x1+x2>4,试判断y1与y2的大小,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系内,以原点O为圆心,1为半径作圆,点P在直线![]() 上运动,过点P作该圆的一条切线,切点为A,则PA的最小值为
上运动,过点P作该圆的一条切线,切点为A,则PA的最小值为![]()
![]()
A. 3 B. 2 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一种品牌羽绒服和防寒服,其中羽绒服的售价是防寒服售价的5倍还多100元,2014年1月份(春节前期)共销售500件,羽绒服与防寒服销量之比是4:1,销售总收入为58.6万元.
(1)求羽绒服和防寒服的售价;
(2)春节后销售进入淡季,2014年2月份羽绒服销量下滑了6m%,售价下滑了4m%,防寒服销量和售价都维持不变,结果销售总收入下降为16.04万元,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com