
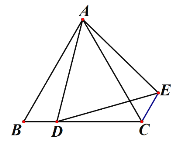
【题目】如图,点D是等边三角形ABC的边BC上一点,以AD为边作等边△ADE,连接CE.
(1)求证:![]() ;
;
(2)若∠BAD=20°,求∠AEC的度数.
【答案】(1)见解析;(2)100°.
【解析】
(1)根据△ADE与△ABC都是等边三角形,得到AC=AB,AE=AD,∠DAE=∠BAC=60°,从而得到∠DAE+∠CAD=∠BAC+∠CAD,即∠CAE=∠BAD,利用SAS证得△ABD≌△ACE;
(2)由△ABD≌△ACE,得到∠ACE=∠B=60°,∠BAD=∠CAE=20°,再由三角形内角和为180°即可求出∠AEC的度数.
(1)证明:∵△ADE与△ABC都是等边三角形,
∴AC=AB,AE=AD,∠DAE=∠BAC=60°,
∴∠DAE+∠CAD=∠BAC+∠CAD,
即∠CAE=∠BAD,
在△CAE与△BAD中, ,
,
∴△ABD≌△ACE(SAS);
(2)∵△ABD≌△ACE,
∴∠ACE=∠B=60°,∠BAD=∠CAE=20°,
∴∠AEC=180°-60°-20°=100°.


科目:初中数学 来源: 题型:
【题目】已知⊙O,请用无刻度的直尺完成下列作图.
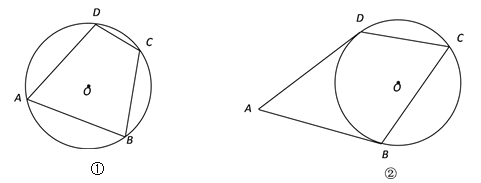
(1)如图①,四边形ABCD是⊙O的内接四边形,且AB=AD,画出∠BCD的角平分线;
(2)如图②,AB和AD是⊙O的切线,切点分别是B、D,点C在⊙O上,画出∠BCD的角平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种成本为40元![]() 千克的商品,若按50元
千克的商品,若按50元![]() 千克销售,一个月可售出500千克,现打算涨价销售,据市场调查,涨价x元时,月销售量为m千克,m是x的一次函数,部分数据如下表:
千克销售,一个月可售出500千克,现打算涨价销售,据市场调查,涨价x元时,月销售量为m千克,m是x的一次函数,部分数据如下表:

![]() 观察表中数据,直接写出m与x的函数关系式:_______________:当涨价5元时,计算可得月销售利润是___________元;
观察表中数据,直接写出m与x的函数关系式:_______________:当涨价5元时,计算可得月销售利润是___________元;
![]() 当售价定多少元时,会获得月销售最大利润,求出最大利润.
当售价定多少元时,会获得月销售最大利润,求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2+2x﹣3.
(1)把函数配成y=a(x﹣h)2+k的形式;
(2)求函数与x轴交点坐标;
(3)用五点法画函数图象
x | … | … | |||||
y | … | … |
(4)当y>0时,则x的取值范围为_____.
(5)当﹣3<x<0时,则y的取值范围为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 阅读:我们约定,在平面直角坐标系中,经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线,叫该点的“特征线”.例如,点M(1,3)的特征线有:x=1,y=3,y=x+2,y=﹣x+4.
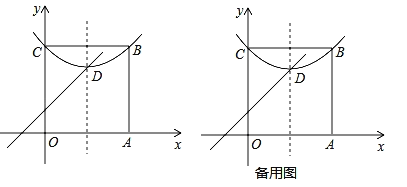
问题与探究:如图,在平面直角坐标系中有正方形OABC,点B在第一象限,A、C分别在x轴和y轴上,抛物线![]() 经过B、C两点,顶点D在正方形内部.
经过B、C两点,顶点D在正方形内部.
(1)直接写出点D(m,n)所有的特征线;
(2)若点D有一条特征线是y=x+1,求此抛物线的解析式;
(3)点P是AB边上除点A外的任意一点,连接OP,将△OAP沿着OP折叠,点A落在点A′的位置,当点A′在平行于坐标轴的D点的特征线上时,满足(2)中条件的抛物线向下平移多少距离,其顶点落在OP上?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数y=![]() 的图象与性质.小美根据学习函数的经验,对函数y=
的图象与性质.小美根据学习函数的经验,对函数y=![]() 的图象与性质进行了探究下面是小美的探究过程,请补充完整:
的图象与性质进行了探究下面是小美的探究过程,请补充完整:
(1)函数y=![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x | -2 | - | -1 | - |
|
| 1 | 2 | 3 | 4 | … |
y | 0 | - | -1 | - |
|
| td style="width:28.95pt; border-top-style:solid; border-top-width:0.75pt; border-right-style:solid; border-right-width:0.75pt; border-left-style:solid; border-left-width:0.75pt; padding:3.38pt 5.03pt; vertical-align:middle">m |
|
| … |
求m的值;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;

(4)结合函数的图象,写出该函数的一条性质: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小龙虾养殖大户为了更好地发挥技术优势,一次性收购了20000kg小龙虾,计划养殖一段时间后再出售.已知每天放养的费用相同,放养10天的总成本为30.4万元;放养20天的总成本为30.8万元(总成本=放养总费用+收购成本).
(1)设每天的放养费用是a万元,收购成本为b万元,求a和b的值;
(2)设这批小龙虾放养t天后的质量为m(kg),销售单价为y元/kg.根据以往经验可知:m与t的函数关系为![]() ;y与t的函数关系如图所示.
;y与t的函数关系如图所示.
①分别求出当0≤t≤50和50<t≤100时,y与t的函数关系式;
②设将这批小龙虾放养t天后一次性出售所得利润为W元,求当t为何值时,W最大?并求出最大值.(利润=销售总额﹣总成本)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某新建火车站站前广场需要绿化的面积为46000米2,施工队在绿化了22000米2后,将每天的工作量增加为原来的1.5倍,结果提前4天完成了该项绿化工程.
(1)该项绿化工程原计划每天完成多少米2?
(2)该项绿化工程中有一块长为20米,宽为8米的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为56米2,两块绿地之间及周边留有宽度相等的人行通道(如图所示),问人行通道的宽度是多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x一元二次方程x2-2(k+1)x+k2-2k-3=0有两个不相等的实数根
(1)求k取值范围;
(2)当k最小的整数时,求抛物线 y= x2-2(k+1)x+k2-2k-3的顶点坐标以及它与x轴的交点坐标;
(3)将(2)中求得的抛物线在x轴下方的部分沿x轴翻折到x轴上方,图象的其余部分不变,得到一个新图象.请你画出这个新图象,并求出新图象与直线 y=x+m有三个不同公共点时m值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com