
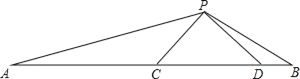
【题目】如图:△PCD是等腰直角三角形,∠DPC=90°,∠APB=135°
求证:(1)△PAC∽△BPD;
(2)若AC=3,BD=1,求CD的长.
 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BC=30,高AD=18,作矩形PQRS,使得P,S分别落在AB,AC边上,Q,R落在BC边上.
(1)求证:△APS ∽△ABC;
(2)如果矩形PQRS是正方形,求它的边长;
(3)如果AP∶PB=1∶2,求矩形PQRS的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
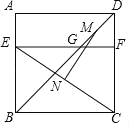
【题目】如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD,CD于点G,F两点,若M,N分别是DG,CE的中点,则MN的长是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
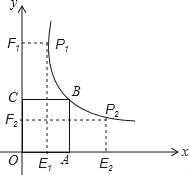
【题目】如图,正方形OABC的面积为9,点O为坐标原点,点A在x轴上,点C上y轴上,点B在反比例函数y=![]() (k>0,x>0)的图象上,点E从原点O出发,以每秒1个单位长度的速度向x轴正方向运动,过点E作x的垂线,交反比例函数y=
(k>0,x>0)的图象上,点E从原点O出发,以每秒1个单位长度的速度向x轴正方向运动,过点E作x的垂线,交反比例函数y=![]() (k>0,x>0)的图象于点P,过点P作PF⊥y轴于点F;记矩形OEPF和正方形OABC不重合部分的面积为S,点E的运动时间为t秒.
(k>0,x>0)的图象于点P,过点P作PF⊥y轴于点F;记矩形OEPF和正方形OABC不重合部分的面积为S,点E的运动时间为t秒.
(1)求该反比例函数的解析式.
(2)求S与t的函数关系式;并求当S=![]() 时,对应的t值.
时,对应的t值.
(3)在点E的运动过程中,是否存在一个t值,使△FBO为等腰三角形?若有,有几个,写出t值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年“雾霾”成为全社会关注的话题某校环保志愿者小组对该市2018年空气质量进行调查,从全年365天中随机抽查了50天的空气质量指数(AQI),得到以下数据:43、62、80、78、46、78、23、59、32、78、86、125、98、116、86、69、28、43、58、87、75、116、178、146、57、26、43、59、77、103、126、159、201、289、315、253、196、102、93、72、56、43、39、44、47、34、31、29、43、52.
(1)请你完成如下的统计表;
AQI | 0~50 | 51~100 | 101~150 | 151~200 | 201~250 | 300以上 |
质量等级 | A(优) | B(良) | C(轻度污染) | D(中度污染) | E(重度污染) | F(严重污染) |
天数 |
(2)请你根据题中所给信息绘制该市2018年空气质量等级条形统计图;
(3)请你估计该市全年空气质量等级为“重度污染”和“严重污染”的天数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 经过点A(
经过点A(![]() ,0),B(
,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,点E、F分别是边BC、CD上的点,且CE=CF,连接AE,AF,取AE的中点M,EF的中点N,连接BM,MN.
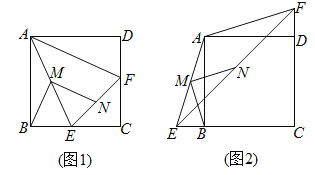
(1)请判断线段BM与MN的数量关系和位置关系,并予以证明.
(2)如图2,若点E在CB的延长线上,点F在CD的延长线上,其他条件不变,(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A、B分别是x轴、y轴上的动点,点C、D是某个函数图象上的点,当四边形ABCD(A、B、C、D各点依次排列)为正方形时,称这个正方形为此函数图象的伴侣正方形。如图,正方形ABCD是一次函数y=x+1图象的其中一个伴侣正方形.
(1)若某函数是一次函数y=x+1,求它的图象的所有伴侣正方形的边长;
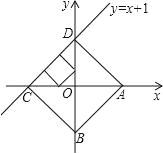
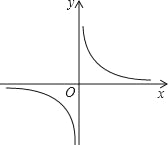
(2)若某函数是反比例函数![]() (k>0),它的图象的伴侣正方形为ABCD,点D(2,m)(m<2)在反比例函数图象上,求m的值及反比例函数解析式;
(k>0),它的图象的伴侣正方形为ABCD,点D(2,m)(m<2)在反比例函数图象上,求m的值及反比例函数解析式;
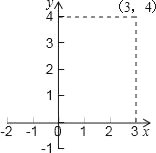
(3)若某函数是二次函数y=ax2+c(a≠0),它的图象的伴侣正方形为ABCD,C、D中的一个点坐标为(3,4).写出伴侣正方形在抛物线上的另一个顶点坐标_____,写出符合题意的其中一条抛物线解析式_____,并判断你写出的抛物线的伴侣正方形的个数是奇数还是偶数?_____.(本小题只需直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知方程组![]() 的解满足
的解满足![]() 为非正数,
为非正数,![]() 为负数.
为负数.
(1)求![]() 的取值范围;
的取值范围;
(2)化简:![]() .
.
(3)在m的取值范围内,当m取何整数时,不等式2mx+x>2m+1的解为x<1?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com