
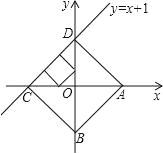
【题目】已知点A、B分别是x轴、y轴上的动点,点C、D是某个函数图象上的点,当四边形ABCD(A、B、C、D各点依次排列)为正方形时,称这个正方形为此函数图象的伴侣正方形。如图,正方形ABCD是一次函数y=x+1图象的其中一个伴侣正方形.
(1)若某函数是一次函数y=x+1,求它的图象的所有伴侣正方形的边长;
(2)若某函数是反比例函数![]() (k>0),它的图象的伴侣正方形为ABCD,点D(2,m)(m<2)在反比例函数图象上,求m的值及反比例函数解析式;
(k>0),它的图象的伴侣正方形为ABCD,点D(2,m)(m<2)在反比例函数图象上,求m的值及反比例函数解析式;
(3)若某函数是二次函数y=ax2+c(a≠0),它的图象的伴侣正方形为ABCD,C、D中的一个点坐标为(3,4).写出伴侣正方形在抛物线上的另一个顶点坐标_____,写出符合题意的其中一条抛物线解析式_____,并判断你写出的抛物线的伴侣正方形的个数是奇数还是偶数?_____.(本小题只需直接写出答案)
【答案】(1)![]() ;(2)
;(2)![]() ;(3)(﹣1,3);(7,﹣3);(﹣4,7);(4,1),对应的抛物线分别为
;(3)(﹣1,3);(7,﹣3);(﹣4,7);(4,1),对应的抛物线分别为![]() ;
;![]() ;
;![]() ,偶数.
,偶数.
【解析】
(1)设正方形ABCD的边长为a,当点A在x轴负半轴、点B在y轴正半轴上时,可知3a=![]() ,求出a,
,求出a,
(2)作DE、CF分别垂直于x、y轴,可知ADE≌△BAO≌△CBF,列出m的等式解出m,
(3)本问的抛物线解析式不止一个,求出其中一个.
解:(1)∵正方形ABCD是一次函数y=x+1图象的其中一个伴侣正方形.
当点A在x轴正半轴、点B在y轴负半轴上时,
∴AO=1,BO=1,
∴正方形ABCD的边长为![]() ,
,
当点A在x轴负半轴、点B在y轴正半轴上时,
设正方形的边长为a,得3a=![]() ,
,
∴![]() ,
,
所以伴侣正方形的边长为![]() 或
或![]() ;
;
(2)作DE、CF分别垂直于x、y轴,
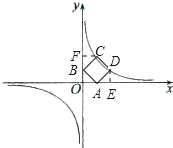
知△ADE≌△BAO≌△CBF,
此时,m<2,DE=OA=BF=m
OB=CF=AE=2﹣m
∴OF=BF+OB=2
∴C点坐标为(2﹣m,2),
∴2m=2(2﹣m)
解得m=1,
反比例函数的解析式为y=![]() ,
,
(3)根据题意画出图形,如图所示:
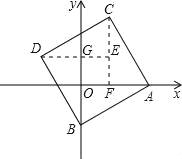
过C作CF⊥x轴,垂足为F,过D作DE⊥CF,垂足为E,
∴△CED≌△DGB≌△AOB≌△AFC,
∵C(3,4),即CF=4,OF=3,
∴EG=3,DE=4,故DG=DE﹣GE=DE﹣OF=4﹣3=1,
则D坐标为(﹣1,3);
设过D与C的抛物线的解析式为:y=ax2+b,
把D和C的坐标代入得:![]() ,
,
解得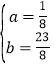 ,
,
∴满足题意的抛物线的解析式为y=![]() x2+
x2+![]() ;
;
同理可得D的坐标可以为:(7,﹣3);(﹣4,7);(4,1),;
对应的抛物线分别为![]() ;
;![]() ;
;![]() ,
,
所求的任何抛物线的伴侣正方形个数为偶数.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
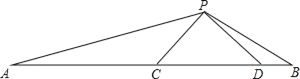
【题目】如图:△PCD是等腰直角三角形,∠DPC=90°,∠APB=135°
求证:(1)△PAC∽△BPD;
(2)若AC=3,BD=1,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂商投产一种新型电子产品,每件制造成本为18元,试销过程中发现,每月销售量y(万件)与销售单价x(元)之间的关系可以近似地看作一次函数y=-2x+100.(利润=售价-制造成本)
(1)写出每月的利润z(万元)与销售单价x(元)之间的函数关系式;
(2)当销售单价为多少元时,厂商每月能获得350万元的利润?当销售单价为多少元时,厂商每月能获得最大利润?最大利润是多少?
(3)根据相关部门规定,这种电子产品的销售单价不能高于32元,如果厂商要获得每月不低于350万元的利润,那么制造出这种产品每月的最低制造成本需要多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
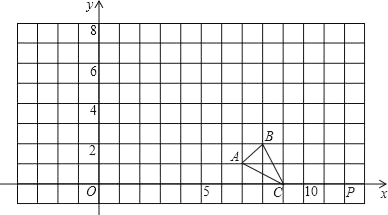
【题目】如图,在直角坐标系中△ABC的A、B、C三点坐标为A(7,1)、B(8,2)、C(9,0).
(1)请在图中画出△ABC的一个以点P(12,0)为位似中心,相似比为3的位似图形△A′B′C′(要求与△ABC同在P点一侧),画出△A′B′C′关于y轴对称的△A′'B′'C′';
(2)写出点A'的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,O是矩形ABCD的对角线AC的中点,E是线段AD上的一点,作OF⊥OE于点O,交直线CD于点F,连结EF,若EF=2CF=2,则AE=_____.
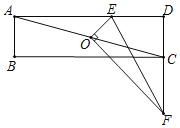
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,连接CD.过E作EF∥DC交BC的延长线于F.
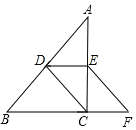
(1)证明:四边形CDEF是平行四边形;
(2)若四边形CDEF的周长是18cm,AC的长为6cm,求线段AB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
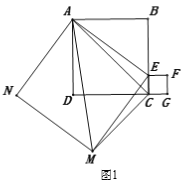
【题目】如图1,三个正方形ABCD、AEMN、CEFG,其中顶点D、C、G在同一条直线上,点E是BC边上的动点,连结AC、AM.
(1)求证:△ACM∽△ABE.
(2)如图2,连结BD、DM、MF、BF,求证:四边形BFMD是平行四边形.
(3)若正方形ABCD的面积为36,正方形CEFG的面积为4,求五边形ABFMN的面积.
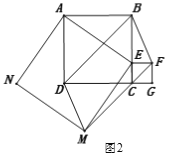
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
为宣传社会主义核心价值观,某社区居委会计划制作1200个大小相同的宣传栏.现有甲、乙两个广告公司都具备制作能力,居委会派出相关人员分别到这两个广告公司了解情况,获得如下信息:
信息一:甲公司单独制作完成这批宣传栏比乙公司单独制作完成这批宣传栏多用10天;
信息二:乙公司每天制作的数量是甲公司每天制作数量的1.2倍.
根据以上信息,求甲、乙两个广告公司每天分别能制作多少个宣传栏?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com