
【题目】如图,△ABC和△ADE都是等腰直角三角形,CE与BD相交于点M,BD交AC于点N.
(1)证明:BD=CE;
(2)证明:BD⊥CE.
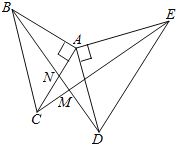
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)要证明BD=CE,只要证明△ABD≌△ACE即可,两三角形中,已知的条件有AD=AE,AB=AC,那么只要再得出两对应边的夹角相等即可得出三角形全等的结论.我们发现∠BAD和∠EAC都是90°加上一个
∠CAD,因此∠CAE=∠BAD.由此构成了两三角形全等中的(SAS)因此两三角形全等.
(2)要证BD⊥CE,只要证明∠BMC是个直角就行了.由(1)得出的全等三角形我们可知:
∠ABN=∠ACE,三角形ABC中,∠ABN+∠CBN+∠BCN=90°,根据上面的相等角,我们可得出∠ACE+∠CBN+∠BCN=90°,即∠ABN+∠ACE=90°,因此∠BMC就是直角.
证明:(1)∵∠BAC=∠DAE=90°
∴∠BAC+∠CAD=∠DAE+∠CAD
即∠CAE=∠BAD
在△ABD和△ACE中
∴△ABD≌△ACE(SAS)
∴BD=CE
(2)∵△ABD≌△ACE
∴∠ABN=∠ACE
∵∠ANB=∠CND
∴∠ABN+∠ANB=∠CND+∠NCE=90°
∴∠CMN=90°
即BD⊥CE.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,CD⊥AB于点D,∠A=30°,以下说法错误的是( )
A. AC=2CDB. AD=2CDC. AD=3BDD. AB=2BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BC=30,高AD=18,作矩形PQRS,使得P,S分别落在AB,AC边上,Q,R落在BC边上.
(1)求证:△APS ∽△ABC;
(2)如果矩形PQRS是正方形,求它的边长;
(3)如果AP∶PB=1∶2,求矩形PQRS的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
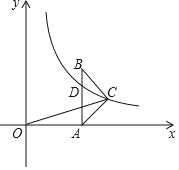
【题目】如图,在△ABC中,AC=BC,AB⊥x轴于A,反比例函数y=![]() (x>0)的图象经过点C,交AB于点D,已知AB=4,BC=
(x>0)的图象经过点C,交AB于点D,已知AB=4,BC=![]() .
.
(1)若OA=4,求k的值.
(2)连接OC,若AD=AC,求CO的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A是一次函数y=![]() x(x≥0)图象上一点,过点A作x轴的垂线l,B是l上一点(B在A上方),在AB的右侧以AB为斜边作等腰直角三角形ABC,反比例函数y=
x(x≥0)图象上一点,过点A作x轴的垂线l,B是l上一点(B在A上方),在AB的右侧以AB为斜边作等腰直角三角形ABC,反比例函数y=![]() (x>0)的图象过点B,C,若△OAB的面积为5,则△ABC的面积是________.
(x>0)的图象过点B,C,若△OAB的面积为5,则△ABC的面积是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F.
(1)求证:AB=CF;
(2)当BC与AF满足什么数量关系时,四边形ABFC是矩形,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
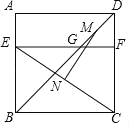
【题目】如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD,CD于点G,F两点,若M,N分别是DG,CE的中点,则MN的长是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
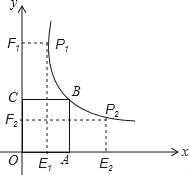
【题目】如图,正方形OABC的面积为9,点O为坐标原点,点A在x轴上,点C上y轴上,点B在反比例函数y=![]() (k>0,x>0)的图象上,点E从原点O出发,以每秒1个单位长度的速度向x轴正方向运动,过点E作x的垂线,交反比例函数y=
(k>0,x>0)的图象上,点E从原点O出发,以每秒1个单位长度的速度向x轴正方向运动,过点E作x的垂线,交反比例函数y=![]() (k>0,x>0)的图象于点P,过点P作PF⊥y轴于点F;记矩形OEPF和正方形OABC不重合部分的面积为S,点E的运动时间为t秒.
(k>0,x>0)的图象于点P,过点P作PF⊥y轴于点F;记矩形OEPF和正方形OABC不重合部分的面积为S,点E的运动时间为t秒.
(1)求该反比例函数的解析式.
(2)求S与t的函数关系式;并求当S=![]() 时,对应的t值.
时,对应的t值.
(3)在点E的运动过程中,是否存在一个t值,使△FBO为等腰三角形?若有,有几个,写出t值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A、B分别是x轴、y轴上的动点,点C、D是某个函数图象上的点,当四边形ABCD(A、B、C、D各点依次排列)为正方形时,称这个正方形为此函数图象的伴侣正方形。如图,正方形ABCD是一次函数y=x+1图象的其中一个伴侣正方形.
(1)若某函数是一次函数y=x+1,求它的图象的所有伴侣正方形的边长;
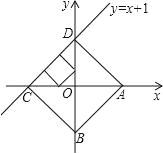
(2)若某函数是反比例函数![]() (k>0),它的图象的伴侣正方形为ABCD,点D(2,m)(m<2)在反比例函数图象上,求m的值及反比例函数解析式;
(k>0),它的图象的伴侣正方形为ABCD,点D(2,m)(m<2)在反比例函数图象上,求m的值及反比例函数解析式;
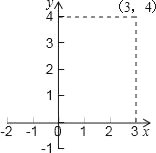
(3)若某函数是二次函数y=ax2+c(a≠0),它的图象的伴侣正方形为ABCD,C、D中的一个点坐标为(3,4).写出伴侣正方形在抛物线上的另一个顶点坐标_____,写出符合题意的其中一条抛物线解析式_____,并判断你写出的抛物线的伴侣正方形的个数是奇数还是偶数?_____.(本小题只需直接写出答案)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com