
【题目】如图,在△ABC中,BC=30,高AD=18,作矩形PQRS,使得P,S分别落在AB,AC边上,Q,R落在BC边上.
(1)求证:△APS ∽△ABC;
(2)如果矩形PQRS是正方形,求它的边长;
(3)如果AP∶PB=1∶2,求矩形PQRS的面积.

【答案】(1)详见解析;(2)正方形PQRS的边长为![]() ;(3)S矩形PQRS=120.
;(3)S矩形PQRS=120.
【解析】
(1)由四边形PQRS是矩形,可得PS∥QR,即可得:△APS∽△ABC;
(2)由矩形PQRS是正方形,可设PS=x,然后利用相似三角形的对应高的比等于相似比,即可得方程![]() 解此方程即可求得答案;
解此方程即可求得答案;
(3)由相似三角形对应边成比例,即可求得PQ与PS的长,继而可求得矩形PQRS的面积.
(1) 证明:∵四边形PQRS是矩形,
∴PS∥QR,即PS∥BC,
∴△APS ∽△ABC.
(2)解:∵四边形PQRS是正方形,
∴PS=PQ=SR,PS∥QR.
∵AD是△ABC的高,即AD⊥BC,
∴AM⊥PS,即AM是△APS的高.
∵△APS ∽△ABC,
∴ ![]()
设PS=x.
∵BC=30,AD=18,
∴AM=18-x,
![]()
解得![]()
∴正方形PQRS的边长为![]() .
.
(3)解:∵四边形PQRS是矩形,∴PQ⊥QR.
∵AD是△ABC的高,∴AD⊥BC,∴PQ∥AD,
∴△PBQ∽△ABD,
∴.![]()
∵![]()
∴![]()
∴![]()
∵△APS ∽△ABC,
∴![]()
∴![]()
∴S矩形PQRS![]()


科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=![]() (n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(1)求一次函数与反比例函数的解析式;
(2)记两函数图象的另一个交点为E,求△CDE的面积;
(3)直接写出不等式kx+b≤![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在直角坐标系中,点A的坐标为(1,0),以OA为边在第四象限内作等边△AOB,点C为x轴的正半轴上一动点(OC>1),连接BC,以BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.
(1)试问△OBC与△ABD全等吗?并证明你的结论;
(2)随着点C位置的变化,点E的位置是否会发生变化?若没有变化,求出点E的坐标;若有变化,请说明理由;
(3)如图2,以OC为直径作圆,与直线DE分别交于点F、G,设AC=m,AF=n,用含n的代数式表示m
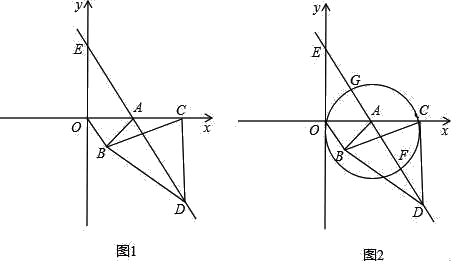
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,解答下列问题.
如图1,已知△ABC中,AD 为中线.延长AD至点E,使 DE=AD.在△ADC和△EDB中,AD=DE,∠ADC=∠EDB,BD=CD,所以,△ACD≌△EBD,进一步可得到AC=BE,AC//BE等结论.
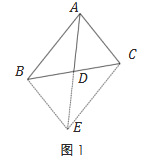
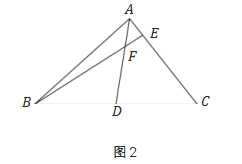
在已知三角形的中线时,我们经常用“倍长中线”的辅助线来构造全等三角形,并进一步解决一些相关的计算或证明题.
解决问题:如图2,在△ABC中,AD是三角形的中线,点F为AD上一点,且BF=AC,连结并延长BF交AC于点E,求证:AE=EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学习小组在讨论“变化的三角形”时,知道大三角形与小三角形是位似图形(如图所示),则小三角形上的顶点(a,b)对应于大三角形上的顶点 ( )

A. (-2a,-2b) B. (2a,2b) C. (-2b,-2a) D. (-2a,-b)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】赵爽(约公元182~250年),我国历史上著名的数学家与天文学家,他详细解释了《周髀算经》中勾股定理,将勾股定理表述为:“勾股各自乘,并之为弦实.开方除之,即弦.”又给出了新的证明方法“赵爽弦图”,巧妙地利用平面解析几何面积法证明了勾股定理.如图所示的“赵爽弦图”是由四个全等的直角三角形和中间一个小正方形拼成的一个大正方形,如果小正方形的面积为1,直角三角形较长直角边长为4,则大正方形的面积为_____________________.
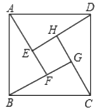
查看答案和解析>>
科目:初中数学 来源: 题型:
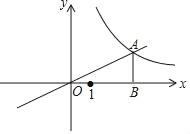
【题目】如图,在平面直角坐标系xOy内,函数y=![]() x的图象与反比例函数y=
x的图象与反比例函数y=![]() (k≠0)图象有公共点A,点A的坐标为(4,a),AB⊥x轴,垂足为点B.
(k≠0)图象有公共点A,点A的坐标为(4,a),AB⊥x轴,垂足为点B.
(1)求反比例函数的解析式;
(2)点C是第一象限内直线OA上一点,过点C作直线CD∥AB,与反比例函数y=![]() (k≠0)的图象交于点D,且点C在点D的上方,CD=
(k≠0)的图象交于点D,且点C在点D的上方,CD=![]() AB,求点D的坐标.
AB,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
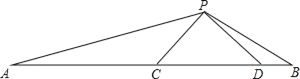
【题目】如图:△PCD是等腰直角三角形,∠DPC=90°,∠APB=135°
求证:(1)△PAC∽△BPD;
(2)若AC=3,BD=1,求CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com