
【题目】如图1,三个正方形ABCD、AEMN、CEFG,其中顶点D、C、G在同一条直线上,点E是BC边上的动点,连结AC、AM.
(1)求证:△ACM∽△ABE.
(2)如图2,连结BD、DM、MF、BF,求证:四边形BFMD是平行四边形.
(3)若正方形ABCD的面积为36,正方形CEFG的面积为4,求五边形ABFMN的面积.
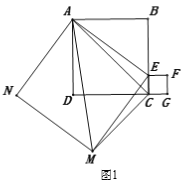
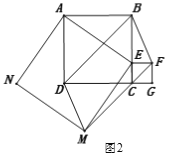
【答案】(1)证明见解析;(2)证明见解析;(3)74.
【解析】
(1)根据四边形ABCD和四边形AEMN都是正方形得![]() ,∠CAB=∠MAC=45°,∠BAE=∠CAM,可证△ACM∽△ABE;
,∠CAB=∠MAC=45°,∠BAE=∠CAM,可证△ACM∽△ABE;
(2)连结AC,由△ACM∽△ABE得∠ACM=∠B=90°,易证∠MCD=∠BDC=45°,得BD∥CM,由MC=![]() BE,FC=
BE,FC=![]() CE,得MF=BD,从而可以证明四边形BFMD是平行四边形;
CE,得MF=BD,从而可以证明四边形BFMD是平行四边形;
(3)根据S五边形ABFMN=S正方形AEMN+S梯形ABFE+S三角形EFM求解即可.
(1)证明:∵四边形ABCD和四边形AEMN都是正方形,
∴![]() ,∠CAB=∠MAC=45°,
,∠CAB=∠MAC=45°,
∴∠CAB-∠CAE=∠MAC-∠CAE,
∴∠BAE=∠CAM,
∴△ACM∽△ABE.
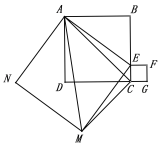
(2)证明:连结AC
因为△ACM∽△ABE,则∠ACM=∠B=90°,
因为∠ACB=∠ECF=45°,
所以∠ACM+∠ACB+∠ECF=180°,
所以点M,C,F在同一直线上,所以∠MCD=∠BDC=45°,
所以BD平行MF,
又因为MC=![]() BE,FC=
BE,FC=![]() CE,
CE,
所以MF=![]() BC=BD,
BC=BD,
所以四边形BFMD是平行四边形
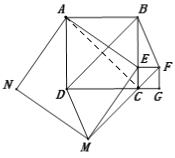
(3)S五边形ABFMN=S正方形AEMN+S梯形ABFE+S三角形EFM
=62+42+![]() (2+6)
(2+6)![]() 4+
4+![]()
![]() 2
2![]() 6
6
=74.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
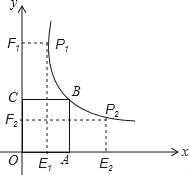
【题目】如图,正方形OABC的面积为9,点O为坐标原点,点A在x轴上,点C上y轴上,点B在反比例函数y=![]() (k>0,x>0)的图象上,点E从原点O出发,以每秒1个单位长度的速度向x轴正方向运动,过点E作x的垂线,交反比例函数y=
(k>0,x>0)的图象上,点E从原点O出发,以每秒1个单位长度的速度向x轴正方向运动,过点E作x的垂线,交反比例函数y=![]() (k>0,x>0)的图象于点P,过点P作PF⊥y轴于点F;记矩形OEPF和正方形OABC不重合部分的面积为S,点E的运动时间为t秒.
(k>0,x>0)的图象于点P,过点P作PF⊥y轴于点F;记矩形OEPF和正方形OABC不重合部分的面积为S,点E的运动时间为t秒.
(1)求该反比例函数的解析式.
(2)求S与t的函数关系式;并求当S=![]() 时,对应的t值.
时,对应的t值.
(3)在点E的运动过程中,是否存在一个t值,使△FBO为等腰三角形?若有,有几个,写出t值.
查看答案和解析>>
科目:初中数学 来源: 题型:
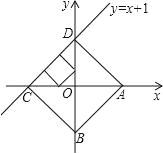
【题目】已知点A、B分别是x轴、y轴上的动点,点C、D是某个函数图象上的点,当四边形ABCD(A、B、C、D各点依次排列)为正方形时,称这个正方形为此函数图象的伴侣正方形。如图,正方形ABCD是一次函数y=x+1图象的其中一个伴侣正方形.
(1)若某函数是一次函数y=x+1,求它的图象的所有伴侣正方形的边长;
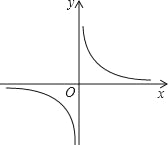
(2)若某函数是反比例函数![]() (k>0),它的图象的伴侣正方形为ABCD,点D(2,m)(m<2)在反比例函数图象上,求m的值及反比例函数解析式;
(k>0),它的图象的伴侣正方形为ABCD,点D(2,m)(m<2)在反比例函数图象上,求m的值及反比例函数解析式;
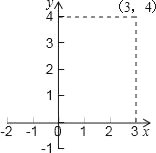
(3)若某函数是二次函数y=ax2+c(a≠0),它的图象的伴侣正方形为ABCD,C、D中的一个点坐标为(3,4).写出伴侣正方形在抛物线上的另一个顶点坐标_____,写出符合题意的其中一条抛物线解析式_____,并判断你写出的抛物线的伴侣正方形的个数是奇数还是偶数?_____.(本小题只需直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,E为射线BC上一点,DF⊥AE于F,连接DE.
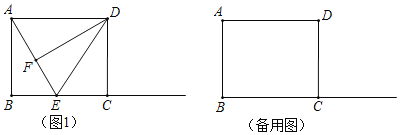
(1)如图1,若E在线段BC上,且CE=EF,求证:AD=AE;
(2)若AB=6,AD=10,在点E的运动过程中,连接BF.
①当△ABF是以AB为底的等腰三角形时,求BE的长;
②当BF∥DE时,若S△ADF=m,S△DCE=n,探究m﹣n的值并简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅游景点门票是50元,凡购买5张门票以上(含5张),景点售票处推出两种优惠销售办法,第一种:“3张按原价,其余按原价的七折优惠”;第二种:“全部按原价的八折优惠”.
问:(1)购买门票张数在什么范围选用第二种优惠办法;
(2)若购10张门票,则选用哪种方法费用较少(请写出理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,函数y=﹣2x+2的图象分别与x轴,y轴交于A,B两点,点C在第一象限,AC⊥AB,且AC=AB,则点C的坐标为( )
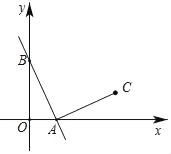
A. (2,1) B. (1,2) C. (1,3) D. (3,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知方程组![]() 的解满足
的解满足![]() 为非正数,
为非正数,![]() 为负数.
为负数.
(1)求![]() 的取值范围;
的取值范围;
(2)化简:![]() .
.
(3)在m的取值范围内,当m取何整数时,不等式2mx+x>2m+1的解为x<1?
查看答案和解析>>
科目:初中数学 来源: 题型:
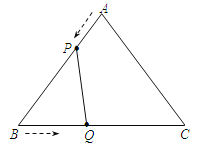
【题目】如图,在△ABC中,AB=AC=10厘米,BC=12厘米,点P从点A出发,沿AB边以1厘米/秒的速度向点B匀速移动;点Q从点B出发,沿BC边以2厘米/秒的速度向点C匀速移动.如果P、Q同时出发,当Q点到达C点时,P点随之停止运动.用t(秒)表示移动的时间(0≤t≤6).
(1)当PQ∥AC时,求t的值;
(2)当t为何值时,P、B、Q三点构成直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=14,AD=8,点E是CD的中点,DG平分∠ADC交AB于点G,过点A作AF⊥DG于点F,连接EF,则EF的长为( )
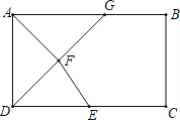
A.3B.4C.5D.6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com