
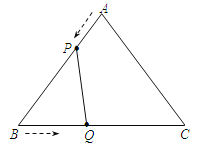
【题目】如图,在△ABC中,AB=AC=10厘米,BC=12厘米,点P从点A出发,沿AB边以1厘米/秒的速度向点B匀速移动;点Q从点B出发,沿BC边以2厘米/秒的速度向点C匀速移动.如果P、Q同时出发,当Q点到达C点时,P点随之停止运动.用t(秒)表示移动的时间(0≤t≤6).
(1)当PQ∥AC时,求t的值;
(2)当t为何值时,P、B、Q三点构成直角三角形.
【答案】(1)t=![]() ;(2)当t为
;(2)当t为![]() 秒或
秒或![]() 秒时,P、B、Q三点构成直角三角形
秒时,P、B、Q三点构成直角三角形
【解析】
(1)根据平行可以得到相似,然后根据相似三角形对应边的比等于相似比求得t值即可;
(2)分∠PQB=90°和∠QPB=90°两种情况分类讨论即可.
(1)∵PQ∥AC,∴△PBQ∽△ABC,∴![]() ,即
,即 ![]() ,解得:t=
,解得:t=![]() (秒);
(秒);
(2)过点A作AD⊥BC于D,如图1.
∵AB=AC,AD⊥BC,∴BD=DC=![]() BC=6.
BC=6.
∵∠B≠90°,∴P、B、Q三点构成直角三角形情况有两种:
①∠PQB=90°,即PQ∥AD,∴![]() ,即
,即 ![]() ,解得:t=
,解得:t=![]() (秒);
(秒);
②∠QPB=90°.而∠ADB=90°,∠B=∠B,∴△BPQ∽△BDA,∴![]() ,即
,即 ![]() ,解得:t=
,解得:t=![]() (秒);
(秒);
综上所述:当t为![]() 秒或
秒或![]() 秒时,P、B、Q三点构成直角三角形.
秒时,P、B、Q三点构成直角三角形.


科目:初中数学 来源: 题型:
【题目】某厂商投产一种新型电子产品,每件制造成本为18元,试销过程中发现,每月销售量y(万件)与销售单价x(元)之间的关系可以近似地看作一次函数y=-2x+100.(利润=售价-制造成本)
(1)写出每月的利润z(万元)与销售单价x(元)之间的函数关系式;
(2)当销售单价为多少元时,厂商每月能获得350万元的利润?当销售单价为多少元时,厂商每月能获得最大利润?最大利润是多少?
(3)根据相关部门规定,这种电子产品的销售单价不能高于32元,如果厂商要获得每月不低于350万元的利润,那么制造出这种产品每月的最低制造成本需要多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
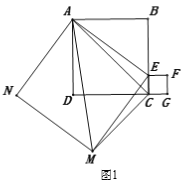
【题目】如图1,三个正方形ABCD、AEMN、CEFG,其中顶点D、C、G在同一条直线上,点E是BC边上的动点,连结AC、AM.
(1)求证:△ACM∽△ABE.
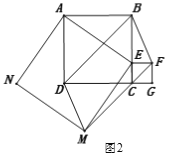
(2)如图2,连结BD、DM、MF、BF,求证:四边形BFMD是平行四边形.
(3)若正方形ABCD的面积为36,正方形CEFG的面积为4,求五边形ABFMN的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
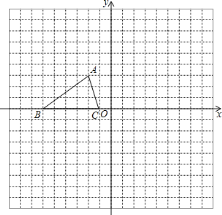
【题目】(1)直接写出A点关于y轴对称的点的坐标是______.
(2)将△ABC向右平移六个单位后得△A1B1C1,则线段AB平移扫过的面积是______.
(3)作出△A1B1C1关于x轴对称的图形△A2B2C2,画出△A2B2C2,连接A2B交y轴于点D,直接写出D点的坐标______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD平分∠BAC,按如下步骤作图:第一步,分别以点A、D为圆心,以大于![]() 的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )
的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )

A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
为宣传社会主义核心价值观,某社区居委会计划制作1200个大小相同的宣传栏.现有甲、乙两个广告公司都具备制作能力,居委会派出相关人员分别到这两个广告公司了解情况,获得如下信息:
信息一:甲公司单独制作完成这批宣传栏比乙公司单独制作完成这批宣传栏多用10天;
信息二:乙公司每天制作的数量是甲公司每天制作数量的1.2倍.
根据以上信息,求甲、乙两个广告公司每天分别能制作多少个宣传栏?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回),商场根据两小球所标金额的和返还相应价格的购物券,可以重新在本商场消费,某顾客刚好消费200元.
(1)该顾客至少可得到_____元购物券,至多可得到_______元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,△ABC中,∠A=90°,D是AC上一点,且∠ADB=2∠C,P是BC上任一点,PE⊥BD于E,PF⊥AC于F.
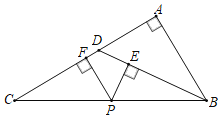
(1)求证:CD=BD;
(2)写出线段AB,PF和PE之间数量关系,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com