
【题目】在矩形ABCD中,E为射线BC上一点,DF⊥AE于F,连接DE.
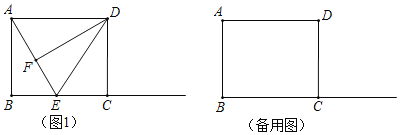
(1)如图1,若E在线段BC上,且CE=EF,求证:AD=AE;
(2)若AB=6,AD=10,在点E的运动过程中,连接BF.
①当△ABF是以AB为底的等腰三角形时,求BE的长;
②当BF∥DE时,若S△ADF=m,S△DCE=n,探究m﹣n的值并简要说明理由.
【答案】(1)见解析;(2)①BE的长是2或18;②m﹣n=0,理由见解析.
【解析】
(1)根据矩形的性质可证△CED≌△FED即可证明;
(2)①分两种情况:当点E在线段BC上时,AF=BF,利用矩形的性质解答即可;当点E在BC延长线上时,AF=BF,利用矩形的性质解答即可;
②当BF∥DE时,延长BF交AD于G,利用三角形的面积和平行四边形的面积之间的关系解答即可.
(1)∵四边形ABCD是矩形,
∴∠DCE=90°,AD∥BC,
∴∠ADE=∠DEC,
∵DF⊥AE
∴∠DCE=∠DFE=90°,
∵CE=EF,DE=DE,
∴△CED≌△FED(HL),
∴∠CED=∠FED,
∴∠ADE=∠AED,
∴AD=AE;
(2)①分两种情况:当点 E 在线段 BC 上时,AF=BF,如图 1 所示:
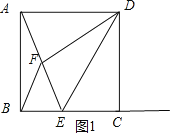
∴∠ABF=∠BAF,
∵∠ABF+∠EBF=90°,
∠BAF+∠BEF=90°,
∴∠EBF=∠BEF,
∴EF=BF,
∴AF=EF,
∵DF⊥AE,
∴DE=AD=10,
在矩形 ABCD 中,CD=AB=6,∠DCE=90°,
∴CE=8,
∴BE=10﹣8=2;
当点 E 在 BC 延长线上时,AF=BF,如图 2 所示:
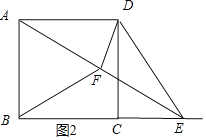
同理可证 AF=EF,
∵DF⊥AE,
∴DE=AD=10,
在矩形 ABCD 中,CD=AB=6,∠DCE=90°,
∴CE=8,
∴BE=10+8=18,
综上,BE的长是2或18;
②m﹣n=0,
理由如下:
当 BF∥DE 时,延长 BF 交 AD 于 G.如图3:
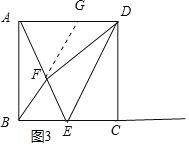
因为四边形ABCD是矩形,
∴AD∥BC,AD=BC,AB=CD,
∠BAG=∠DCE=90°,
∵BF∥DE,
∴四边形 BEDG 是平行四边形,
∴BE=DG,
∴S△DEF=![]() BEDG,AG=CE,
BEDG,AG=CE,
S△BEF+S△DFG=![]() SBEDG,
SBEDG,
∵△ABG≌△CDE,
∴S△ABG=S△CDE,
∵S△ABE=![]() SBEDG,
SBEDG,
∴S△ABE=S△BEF+S△DFG,
∴S△ABF=S△DFG,
∴S△ABF+S△AFG=S△DFG+S△AFG,
即S△ABG=S△ADF,
∴S△CDE=S△ADF,
即m﹣n=0.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
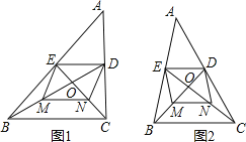
【题目】在△ABC中,BD、CE分别是边AC、AB上的中线,BD与CE交于点O.
(1)如图1,若M、N分别是OB、OC的中点,求证:OB=2OD;
(2)如图2,若BD⊥CE,AB=8,BC=6,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂商投产一种新型电子产品,每件制造成本为18元,试销过程中发现,每月销售量y(万件)与销售单价x(元)之间的关系可以近似地看作一次函数y=-2x+100.(利润=售价-制造成本)
(1)写出每月的利润z(万元)与销售单价x(元)之间的函数关系式;
(2)当销售单价为多少元时,厂商每月能获得350万元的利润?当销售单价为多少元时,厂商每月能获得最大利润?最大利润是多少?
(3)根据相关部门规定,这种电子产品的销售单价不能高于32元,如果厂商要获得每月不低于350万元的利润,那么制造出这种产品每月的最低制造成本需要多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
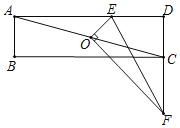
【题目】已知,O是矩形ABCD的对角线AC的中点,E是线段AD上的一点,作OF⊥OE于点O,交直线CD于点F,连结EF,若EF=2CF=2,则AE=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,连接CD.过E作EF∥DC交BC的延长线于F.
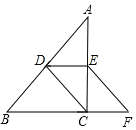
(1)证明:四边形CDEF是平行四边形;
(2)若四边形CDEF的周长是18cm,AC的长为6cm,求线段AB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
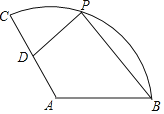
【题目】如图,在扇形CAB中,CA=4,∠CAB=120°,D为CA的中点,P为弧BC上一动点(不与C,B重合),则2PD+PB的最小值为( )
A. ![]() B.
B. ![]() C. 10 D.
C. 10 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,三个正方形ABCD、AEMN、CEFG,其中顶点D、C、G在同一条直线上,点E是BC边上的动点,连结AC、AM.
(1)求证:△ACM∽△ABE.
(2)如图2,连结BD、DM、MF、BF,求证:四边形BFMD是平行四边形.
(3)若正方形ABCD的面积为36,正方形CEFG的面积为4,求五边形ABFMN的面积.
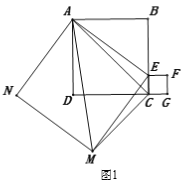
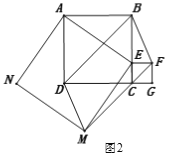
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回),商场根据两小球所标金额的和返还相应价格的购物券,可以重新在本商场消费,某顾客刚好消费200元.
(1)该顾客至少可得到_____元购物券,至多可得到_______元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com