
【题目】如图1,在正方形ABCD中,点E、F分别是边BC、CD上的点,且CE=CF,连接AE,AF,取AE的中点M,EF的中点N,连接BM,MN.
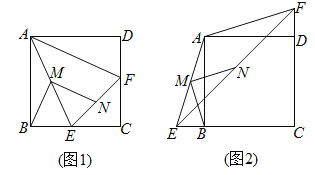
(1)请判断线段BM与MN的数量关系和位置关系,并予以证明.
(2)如图2,若点E在CB的延长线上,点F在CD的延长线上,其他条件不变,(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
【答案】(1)BM=MN,BM⊥MN,证明见解析;(2)仍然成立,证明见解析
【解析】
(1)根据已知正方形ABCD的边角相等关系,推出△ABE≌△ADF(SAS),得出AE=AF,利用MN是△AEF的中位线,BM为Rt△ABE的中线,可得BM=MN,由外角性质,得出∠BME=∠1+∠3,再由MN∥AF,∠1+∠2+∠EAF=∠BAD=90°,等角代换可推出结论;
(2)同(1)思路一样,证明△ABE≌△ADF(SAS),利用外角性质和中位线平行关系,通过等角代换即得证明结论.
(1)BM=MN,BM⊥MN.
证明:在正方形ABCD中,∠BAD=∠ABC=∠ADC=90°,AB=AD=BC=DC,
∵CE=CF,
∴BC-CE=DC-CF,
∴BE=DF,
∴△ABE≌△ADF(SAS),
∴∠1=∠2,AE=AF,
∵M为AE的中点,N为EF的中点,
∴MN是△AEF的中位线,BM为Rt△ABE的中线.
∴MN∥AF,MN=![]() AF,BM=
AF,BM=![]() AE=AM,
AE=AM,
∴BM=MN,∠EMN=∠EAF,
∵BM=AM,
∴∠1=∠3, ∠2=∠3,
∴∠BME=∠1+∠3=∠1+∠2,
∴∠BMN=∠BME+∠EMN=∠1+∠2+∠EAF=∠BAD=90°,
∴BM⊥MN.
故答案为:BM=MN,BM⊥MN.
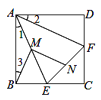
(2)(1)中结论仍然成立.
证明:在正方形ABCD中,∠BAD=∠ABC=∠ADC=90°,AB=AD=BC=DC,
∴∠ABE=∠ADF=90°,
∵CE=CF,∴CE-BC=CF-DC,∴BE=DF,
∴△ABE≌△ADF(SAS),∴∠1=∠2,AE=AF,
同理(1)得MN∥AF,MN=![]() AF,BM=
AF,BM=![]() AE=AM,
AE=AM,
∴BM=MN,
同理(1)得∠BME=∠1+∠2,∠EMN=∠EAF,
∴∠BMN=∠EMN-∠BME=∠EAF-(∠1+∠2)=∠BAD=90°,
∴BM⊥MN,
故答案为:结论仍成立.


科目:初中数学 来源: 题型:
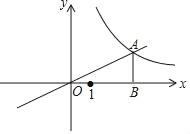
【题目】如图,在平面直角坐标系xOy内,函数y=![]() x的图象与反比例函数y=
x的图象与反比例函数y=![]() (k≠0)图象有公共点A,点A的坐标为(4,a),AB⊥x轴,垂足为点B.
(k≠0)图象有公共点A,点A的坐标为(4,a),AB⊥x轴,垂足为点B.
(1)求反比例函数的解析式;
(2)点C是第一象限内直线OA上一点,过点C作直线CD∥AB,与反比例函数y=![]() (k≠0)的图象交于点D,且点C在点D的上方,CD=
(k≠0)的图象交于点D,且点C在点D的上方,CD=![]() AB,求点D的坐标.
AB,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于G,交BE于H.下列结论:①S△ABE=S△BCE;②∠AFG=∠AGF;③∠FAG=2∠ACF;④BH=CH.其中所有正确结论的序号是

A.①②③④B.①②③C.②④D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
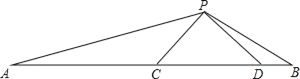
【题目】如图:△PCD是等腰直角三角形,∠DPC=90°,∠APB=135°
求证:(1)△PAC∽△BPD;
(2)若AC=3,BD=1,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人参加射击比赛,两人成绩如图所示.
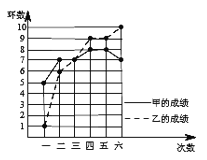
(1)填表:
平均数 | 方差 | 中位数 | 众数 | |
甲 | 7 | 1 | 7 | |
乙 | 9 |
(2)只看平均数和方差,成绩更好的是 .(填“甲”或“乙”)
(3)仅就折线图上两人射击命中环数的走势看,更有潜力的是 .(填“甲”或“乙”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂商投产一种新型电子产品,每件制造成本为18元,试销过程中发现,每月销售量y(万件)与销售单价x(元)之间的关系可以近似地看作一次函数y=-2x+100.(利润=售价-制造成本)
(1)写出每月的利润z(万元)与销售单价x(元)之间的函数关系式;
(2)当销售单价为多少元时,厂商每月能获得350万元的利润?当销售单价为多少元时,厂商每月能获得最大利润?最大利润是多少?
(3)根据相关部门规定,这种电子产品的销售单价不能高于32元,如果厂商要获得每月不低于350万元的利润,那么制造出这种产品每月的最低制造成本需要多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
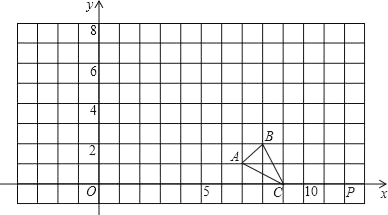
【题目】如图,在直角坐标系中△ABC的A、B、C三点坐标为A(7,1)、B(8,2)、C(9,0).
(1)请在图中画出△ABC的一个以点P(12,0)为位似中心,相似比为3的位似图形△A′B′C′(要求与△ABC同在P点一侧),画出△A′B′C′关于y轴对称的△A′'B′'C′';
(2)写出点A'的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,连接CD.过E作EF∥DC交BC的延长线于F.
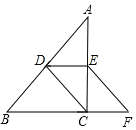
(1)证明:四边形CDEF是平行四边形;
(2)若四边形CDEF的周长是18cm,AC的长为6cm,求线段AB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
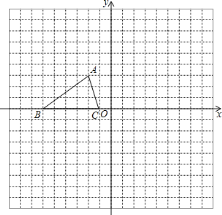
【题目】(1)直接写出A点关于y轴对称的点的坐标是______.
(2)将△ABC向右平移六个单位后得△A1B1C1,则线段AB平移扫过的面积是______.
(3)作出△A1B1C1关于x轴对称的图形△A2B2C2,画出△A2B2C2,连接A2B交y轴于点D,直接写出D点的坐标______ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com