
【题目】如图,在△ABC中,AB=AC,AD⊥BC垂足是D,AN是∠BAC的外角∠CAM的平分线,CE⊥AN,垂足是E,连接DE交AC于F.
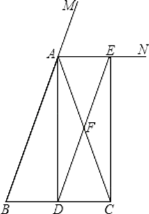
(1)求证:四边形ADCE为矩形;
(2)求证:DF∥AB,DF=![]() ;
;
(3)当△ABC满足什么条件时,四边形ADCE为正方形,简述你的理由.
【答案】(1)见解析;(2)见解析;(3)当△ABC是等腰直角三角形时,四边形ADCE为正方形.见解析
【解析】
(1)先根据AB=AC,AD⊥BC垂足是D,得AD平分∠BAC,然后根据AE是△ABC的外角平分线,可求出AN∥BC,故∠DAE=∠ADC=∠AEC=90°,所以四边形ADCE为矩形;
(2)根据四边形ADCE是矩形,可知F是AC的中点,由AB=AC,AD平分∠BAC可知D是BC的中点,故DF是△ABC的中位线,即DF∥AB,DF=![]() AB;
AB;
(3)根据矩形的性质可知当△ABC是等腰直角三角形时,则∠5=∠2=45°,利用等腰三角形的性质定理可知对应边AD=CD.再运用邻边相等的矩形是正方形.问题得证.
证明:如图
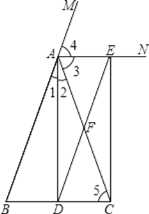
(1)∵AB=AC,AD⊥BC垂足是D,
∴AD平分∠BAC,∠B=∠5,
∴∠1=∠2,
∵AE是△ABC的外角平分线,
∴∠3=∠4,
∵∠1+∠2+∠3+∠4=180°,
∴∠2+∠3=90°,
即∠DAE=90°,
又∵AD⊥BC,
∴∠ADC=90°,
又∵CE⊥AE,
∴∠AEC=90°,
∴四边形ADCE是矩形.
(2)∵四边形ADCE是矩形,
∴AF=CF=![]() AC,
AC,
∵AB=AC,AD平分∠BAC,
∴BD=CD=![]() BC,
BC,
∴DF是△ABC的中位线,
即DF∥AB,DF=![]() .
.
(3)当△ABC是等腰直角三角形时,四边形ADCE为正方形.
∵在Rt△ABC中,AD平分∠BAC
∴∠5=∠2=∠3=45°,
∴AD=CD,
又∵四边形ADCE是矩形,
∴矩形ADCE为正方形.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
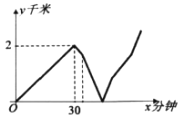
【题目】周末小明匀速步行赶往学校参加学校组织的植树活动,小明从家出发30分钟后,忽然想起没有带植树工具,于是马上掉头往回走行走速度比之前提高了1千米/时(仍保持匀速步行),同时小明打电话给爸爸,请爸爸帮他把植树工具送过来,从小明开始打电话到爸爸出门一共用了4分钟,爸爸的行走速度与此时小明的行走速度相同,两人相遇后,小明立即赶往学校,爸爸则转身回家,两人速度均保持不变,爸爸在回家途中用了10分钟吃早餐,然后立即回家,当爸爸到家时小明刚好到达学校.爸爸和小明相距的路程y(千米)与小明从家出发的时间x(分钟)之间的关系如图所示,求今天早上小明从家到学校途中行走的总路程是________千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,二次函数的图象与x轴交于A(-2,0),B(4,0)两点,且函数的最大值为9.
(1)求二次函数的解析式;

(2)设此二次函数图象的顶点为C,与y轴交点为D,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
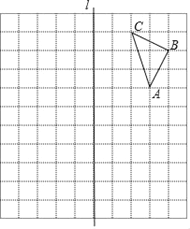
【题目】如图,直线l与△ABC在边长为1个单位长度的小正方形网格中,点A,B,C都为网格线的交点.
(1)请画出△ABC关于直线l对称的△A1B1C1(点A,B,C的对称点分别为A1,B1,C1).
(2)请画出将线段AC向左平移3个单位,再向下平移5个单位得到的线段A2C2(点A,C的对应点分别为A2,C2),再以A2C2为斜边画一个等腰直角三角形A2B2C2.
查看答案和解析>>
科目:初中数学 来源: 题型:
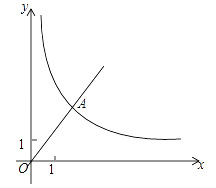
【题目】已知:如图,在平面直角坐标系中,正比例函数y=![]() 的图象经过A,点A的纵坐标为4,反比例函数y=
的图象经过A,点A的纵坐标为4,反比例函数y=![]() 的图象也经过点A,在第一象限内的点B在这个反比例函数图象上,过点B做BC∥x轴,交y轴于点C,且AC=AB,求:
的图象也经过点A,在第一象限内的点B在这个反比例函数图象上,过点B做BC∥x轴,交y轴于点C,且AC=AB,求:
(1)这个反比例函数的解析式;
(2)ΔABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,0),B(0,2),C(2,1);
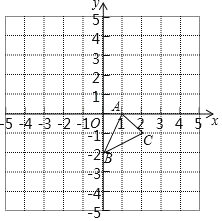
(1)以原点O为位似中心,在第二象限画出△A1B1C1,使△A1B1C1与△ABC的位似比为2:1;
(2)点P(a,b)为线段AC上的任意一点,则点P在△A1B1C1中的对应点P1的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
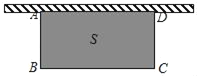
【题目】如图.利用一面墙(墙的长度不限),用20m的篱笆围成一个矩形场地ABCD.设矩形与墙垂直的一边AB=xm,矩形的面积为Sm2.
(1)用含x的式子表示S;
(2)若面积S=48m2,求AB的长;
(3)能围成S=60m2的矩形吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将一块等腰直角三角板(△ABC)按如图所示放置,若AO=2,OC=1,∠ACB=90°.
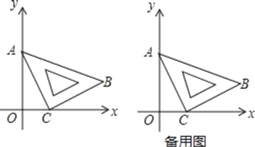
(1)直接写出点B的坐标是 ;
(2)如果抛物线l:y=ax2﹣ax﹣2经过点B,试求抛物线l的解析式;
(3)把△ABC绕着点C逆时针旋转90°后,顶点A的对应点A1是否在抛物线l上?为什么?
(4)在x轴上方,抛物线l上是否存在一点P,使由点A,C,B,P构成的四边形为中心对称图形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解题时,最容易想到的方法未必是最简单的,你可以再想一想,尽量优化解法.
例题呈现
关于x的方程a(x+m)2+b=0的解是x1=1,x2=-2(a、m、b均为常数,a≠0),则方程a(x+m+2)2+b=0的解是 .
解法探讨
(1)小明的思路如图所示,请你按照他的思路解决这个问题;
小明的思路
第1步 把1、-2代入到第1个方程中求出m的值;
第2步 把m的值代入到第1个方程中求出![]() 的值;
的值;
第3步 解第2个方程.
(2)小红仔细观察两个方程,她把第2个方程a(x+m+2)2+b=0中的“x+2”看作第1个方程中的“x”,则“x+2”的值为 ,从而更简单地解决了问题.
策略运用
(3)小明和小红认真思考后发现,利用方程结构的特点,无需计算“根的判别式”就能轻松解决以下问题,请用他们说的方法完成解答.
已知方程 (a2-2b2)x2+(2b2-2c2)x+2c2-a2=0有两个相等的实数根,其中a、b、c是△ABC三边的长,判断△ABC的形状.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com