
،¾جâؤ؟،؟شعئ½أوض±½ا×ّ±êدµضذ£¬½«ز»؟éµبرüض±½اب½ا°ه£¨،÷ABC£©°´بçح¼ثùت¾·إضأ£¬بôAO£½2£¬OC£½1£¬،دACB£½90،م£®
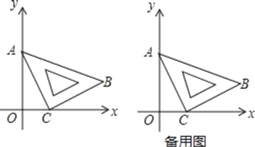
£¨1£©ض±½سذ´³ِµمBµؤ×ّ±êتا،، £»
£¨2£©بç¹ûإ×خïدكl£؛y£½ax2©پax©پ2¾¹µمB£¬تشاَإ×خïدكlµؤ½âخِت½£»
£¨3£©°ر،÷ABCبئ×إµمCؤوت±صëذ×ھ90،م؛َ£¬¶¥µمAµؤ¶شس¦µمA1تا·ٌشعإ×خïدكlةد£؟خھت²أ´£؟
£¨4£©شعxضلةد·½£¬إ×خïدكlةدتا·ٌ´وشعز»µمP£¬ت¹سةµمA£¬C£¬B£¬P¹¹³ةµؤثؤ±كذخخھضذذؤ¶ش³ئح¼ذخ£؟بô´وشع£¬اَ³ِµمPµؤ×ّ±ê£»بô²»´وشع£¬اëثµأ÷ہيسة£®
،¾´ً°¸،؟£¨1£©µمBµؤ×ّ±êخھ£¨3£¬1£©£»£¨2£©y£½![]() x2©پ
x2©پ![]() x©پ2£»£¨3£©µمA1شعإ×خïدكةد£»ہيسة¼û½âخِ£»£¨4£©´وشع£¬µمP£¨©پ2£¬1£©£®
x©پ2£»£¨3£©µمA1شعإ×خïدكةد£»ہيسة¼û½âخِ£»£¨4£©´وشع£¬µمP£¨©پ2£¬1£©£®
،¾½âخِ،؟
£¨1£©ت×دب¹µمB×÷BD،حxضل£¬´¹×مخھD£¬ح¨¹ض¤أ÷،÷BDC،ص،÷COA¼´؟ةµأBD£½OC£½1£¬CD£½OA£½2£¬´س¶ّµأضھB×ّ±ê£»
£¨2£©ہûسأ´¶¨دµت·¨£¬½«B×ّ±ê´ْبë¼´؟ةاَµأ£»
£¨3£©»³ِذ×ھ؛َµؤح¼ذخ£¬¹µم![]() ×÷xضلµؤ´¹دك£¬¹¹شىب«µبب½اذخ£¬اَ³ِ
×÷xضلµؤ´¹دك£¬¹¹شىب«µبب½اذخ£¬اَ³ِ![]() µؤ×ّ±ê´ْبëإ×خïدك½âخِت½¼´؟ة½ّذذإذ¶د£»
µؤ×ّ±ê´ْبëإ×خïدك½âخِت½¼´؟ة½ّذذإذ¶د£»
£¨4£©سةإ×خïدكµؤ½âخِت½دبةè³ِPµؤ×ّ±ê£¬شظ¸ù¾فضذذؤ¶ش³ئµؤذشضت سëدك¶خضذµمµؤ¹«ت½ءذ³ِ·½³جاَ½â¼´؟ة،£
£¨1£©بçح¼1£¬¹µمB×÷BD،حxضل£¬´¹×مخھD£¬
،ك،دBCD+،دACO£½90،م£¬،دAC0+،دOAC£½90،م£¬
،à،دBCD£½،دCAO£¬
سض،ك،دBDC£½،دCOA£½90،م£¬CB£½AC£¬
شع،÷BDC؛ح،÷COAضذ£؛
،ك،دBDC=،دCOA£¬،دBCD£½،دCAO£¬CB=AC£¬
،à،÷BDC،ص،÷COA£¨AAS£©£¬
،àBD£½OC£½1£¬CD£½OA£½2£¬
،àµمBµؤ×ّ±êخھ£¨3£¬1£©£»
£¨2£©،كإ×خïدكy£½ax2©پax©پ2¹µمB£¨3£¬1£©£¬
،à1£½9a©پ3a©پ2£¬
½âµأ£؛a£½![]() £¬
£¬
،àإ×خïدكµؤ½âخِت½خھy£½![]() x2©پ
x2©پ![]() x©پ2£»
x©پ2£»
£¨3£©ذ×ھ؛َبçح¼1ثùت¾£¬¹µمA1×÷A1M،حxضل£¬
،ك°ر،÷ABCبئ×إµمCؤوت±صëذ×ھ90،م£¬
،à،دABC£½،دA1BC£½90،م£¬
،àA1£¬B£¬C¹²دك£¬
شعب½اذخBDC؛حب½اذخA1CMضذ£؛
،ك،دBDC=،دA1MC=90،م£¬،دBCD=،دA1CM£¬A1C=BC,
،à،÷BDC،ص،÷A1CM
،àCM£½CD£½3©پ1£½2£¬A1M£½BD£½1£¬
،àOM£½1£¬
،àµمA1£¨©پ1£¬©پ1£©£¬
°رµمx£½©پ1´ْبëy£½![]() x2©پ
x2©پ![]() x©پ2£¬
x©پ2£¬
y£½©پ1£¬
،àµمA1شعإ×خïدكةد£®
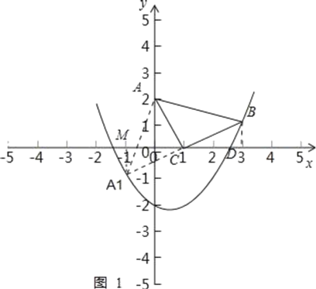
£¨4£©ةèµمP£¨t£¬![]() t2©پ
t2©پ![]() t©پ2£©£¬
t©پ2£©£¬
µمA£¨0£¬2£©£¬µمC£¨1£¬0£©£¬µمB£¨3£¬1£©£¬
بôµمP؛حµمC¶شس¦£¬سةضذذؤ¶ش³ئµؤذشضت؛حدك¶خضذµم¹«ت½؟ةµأ£؛
![]() £¬
£¬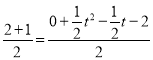 £¬
£¬
خق½â£¬
بôµمP؛حµمA¶شس¦£¬سةضذذؤ¶ش³ئµؤذشضت؛حدك¶خضذµم¹«ت½؟ةµأ£؛
![]() £¬
£¬ £¬
£¬
خق½â£¬
بôµمP؛حµمB¶شس¦£¬سةضذذؤ¶ش³ئµؤذشضت؛حدك¶خضذµم¹«ت½؟ةµأ£؛
![]() £¬
£¬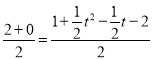 £¬
£¬
½âµأ£؛t£½©پ2£¬
![]() t2©پ
t2©پ![]() t©پ2£½1
t©پ2£½1
ثùزش£؛´وشع£¬µمP£¨©پ2£¬1£©£®


 جىجىدٍةدز»±¾؛أ¾يدµءذ´ً°¸
جىجىدٍةدز»±¾؛أ¾يدµءذ´ً°¸ ذ،ر§ةْ10·ضضسس¦سأجâدµءذ´ً°¸
ذ،ر§ةْ10·ضضسس¦سأجâدµءذ´ً°¸
| ؤ꼶 | ¸كضذ؟خ³ج | ؤ꼶 | ³ُضذ؟خ³ج |
| ¸كز» | ¸كز»أâ·ر؟خ³جحئ¼ِ£، | ³ُز» | ³ُز»أâ·ر؟خ³جحئ¼ِ£، |
| ¸ك¶ | ¸ك¶أâ·ر؟خ³جحئ¼ِ£، | ³ُ¶ | ³ُ¶أâ·ر؟خ³جحئ¼ِ£، |
| ¸كب | ¸كبأâ·ر؟خ³جحئ¼ِ£، | ³ُب | ³ُبأâ·ر؟خ³جحئ¼ِ£، |
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬شع،÷ABCضذ£¬AB£½AC£¬Pتا±كBCµؤضذµم£¬PD،حAB£¬PE،حAC£¬´¹×م·ض±ًخھD،¢E
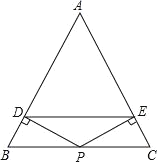
£¨1£©اَض¤£؛PD£½PE£»
£¨2£©DEسëBCئ½ذذآً£؟اëثµأ÷ہيسة£»
£¨3£©اëجي¼سز»¸ِجُ¼£¬ت¹ثؤ±كذخADPEخھص·½ذخ£¬²¢¼سزشض¤أ÷£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬شع،÷ABCضذ£¬AB£½AC£¬AD،حBC´¹×متاD£¬ANتا،دBACµؤحâ½ا،دCAMµؤئ½·ضدك£¬CE،حAN£¬´¹×متاE£¬ء¬½سDE½»ACسعF£®
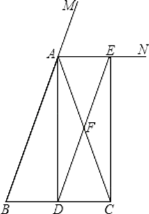
£¨1£©اَض¤£؛ثؤ±كذخADCEخھ¾طذخ£»
£¨2£©اَض¤£؛DF،خAB£¬DF£½![]() £»
£»
£¨3£©µ±،÷ABCآْ×مت²أ´جُ¼ت±£¬ثؤ±كذخADCEخھص·½ذخ£¬¼ٍتِؤمµؤہيسة£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼ثùت¾£¬شعµب±ك،÷ABCضذ£¬µمDتا±كACةدز»µم£¬ء¬½سBD£¬½«،÷BCDبئ×إµمBؤوت±صëذ×ھ60£¬µأµ½،÷BAE£¬ء¬½سED£¬شٍدآءذ½لآغضذ£؛¢ظAE،خBC£»¢ع،دDEB=60£»¢غ،دADE=،دBDC£¬ئنضذصب·½لآغµؤذٍ؛إتا£¨ £©
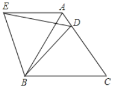
A.¢ظ¢عB.¢ظ¢غC.¢ع¢غD.ض»سذ¢ظ
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬µمDخھ،رOةدز»µم£¬µمCشعض±¾¶BAµؤرس³¤دكةد£¬از،دCDA£½،دCBD£®

£¨1£©إذ¶دض±دكCD؛ح،رOµؤخ»ضأ¹طدµ£¬²¢ثµأ÷ہيسة£»
£¨2£©¹µمB×÷،رOµؤاذدكBE½»ض±دكCDسعµمE£¬بôBE£½5£¬CD£½8£¬اَ،رOµؤ°ë¾¶£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟ز»،¢شؤ¶ء²ؤءد£؛
زرضھتµتm£¬nآْ×م£¨2m2£«n2£«1£©£¨2m2£«n2£1£©=80£¬تشاَ2m2£«n2µؤضµ£®
½â£؛ةè2m2£«n2=t£¬شٍش·½³ج±نخھ£¨t£«1£©£¨t£1£©=80£¬صûہيµأt2£1=80£¬t2=81£¬ثùزشt=حء9£¬زٍخھ2m2£«n2£¾0£¬ثùزش2m2£«n2=9£®
¶،¢·½·¨¹éؤة£؛
ةدأوصâضض·½·¨³ئخھ،°،،،،،،،، ·¨،±£¬°رئنضذؤ³ذ©²؟·ض؟´³ةز»¸ِصûجه£¬²¢سأذآ×ضؤ¸´ْجو£¨¼´»»شھ£©£¬شٍؤـت¹¸´شسµؤختجâ¼ٍµ¥»¯£®
ب،¢ج½ث÷تµ¼ù£؛
¸ù¾فزشةدشؤ¶ء²ؤءدؤعبف£¬½â¾ِدآءذختج⣬²¢ذ´³ِ½â´ً¹³ج£®
£¨1£©زرضھتµتx،¢y£¬آْ×م£¨2x2£«2y2£«3£©£¨2x2£«2y2£3£©=27£¬اَx2£«y2µؤضµ£®
£¨2£©زرضھRt،÷ACBµؤب±كخھa،¢b،¢c£¨cخھذ±±ك£©£¬ئنضذa،¢bآْ×م£¨a2£«b2£©£¨a2£«b2£4£©=5£¬اَRt،÷ACBحâ½سش²µؤ°ë¾¶£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬إ×خïدكy£½ax2£«2x£«c¾¹µمA(0£¬3)£¬B(£1£¬0)£¬اë»ط´ًدآءذختجâ£؛
(1)اَإ×خïدك¶شس¦µؤ¶´خ؛¯تµؤ±ي´ïت½£»
(2)إ×خïدكµؤ¶¥µمخھD£¬¶ش³ئضلسëxضل½»سعµمE£¬ء¬½سBD£¬اَBDµؤ³¤£®
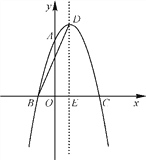
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬ص·½ذخABCDضذ£¬µمEتاAD±كµؤضذµم£¬BD£¬CE½»سعµمH£¬BE،¢AH½»سعµمG£¬شٍدآءذ½لآغ£؛¢ظ،دABE£½،دDCE£»¢عAG،حBE£»¢غS،÷BHE£½S،÷CHD£»¢ـ،دAHB£½،دEHD£®ئنضذصب·µؤتا£¨،،،،£©
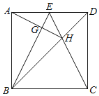
A.¢ظ¢غB.¢ظ¢ع¢غ¢ـC.¢ظ¢ع¢غD.¢ظ¢غ¢ـ
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£؛،÷PCDتاµبرüض±½اب½اذخ£¬،دDPC=90،م£¬،دAPB=135،م
اَض¤£؛£¨1£©،÷PAC،×،÷BPD£»
£¨2£©بôAC=3£¬BD=1£¬اَCDµؤ³¤£®
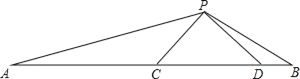
²é؟´´ً°¸؛ح½âخِ>>
¹ْ¼تر§ذ£سإر، - ء·د°²لءذ±ي - تشجâءذ±ي
؛±±ت،»¥ءھحّخ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨ئ½ج¨ | حّةدسذ؛¦ذإد¢¾ظ±¨×¨اّ | µçذإص©ئ¾ظ±¨×¨اّ | ةوہْت·ذéخقض÷زهسذ؛¦ذإد¢¾ظ±¨×¨اّ | ةوئَاضب¨¾ظ±¨×¨اّ
خ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨µç»°£؛027-86699610 ¾ظ±¨ستدن£؛58377363@163.com