
【题目】如图1,在![]() 中,
中,![]() ,
,![]() 为
为![]() 上一点,连接
上一点,连接![]() ,
,![]() .
.
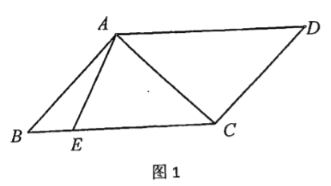
(1)若![]() ,
,![]() ,求
,求![]() 的长;
的长;
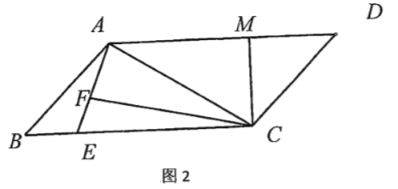
(2)如图2,过![]() 作
作![]() 于
于![]() ,
,![]() 为
为![]() 上一点,
上一点,![]() ,且
,且![]() .求证:
.求证:![]() .
.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
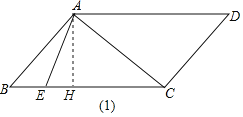
(1)如图(1),过A作AH⊥BC于H,解直角三角形即可得到结论;
(2)如图(2),在AM上截取MN=MC,在△ACF内以AF为底边作等腰直角三角形AFP,连接CP,根据平行线的性质函数三角形的内角和得到∠CAN=∠PAC,求得∠APC=∠FPC=![]() =135°=∠ANC,根据全等三角形的性质得到AP=AN,于是得到结论.
=135°=∠ANC,根据全等三角形的性质得到AP=AN,于是得到结论.
(1)解:过点![]() 作
作![]() 于
于![]()
∵![]() ,
,![]()
∴![]() ,
,![]()
∴![]()
(2)如图(2),在AM上截取MN=MC,在△ACF内以AF为底边作等腰直角三角形AFP,连接CP,

∵∠AFC+∠FAC+∠ACF=180°,∠B+∠FAC+∠BAF+∠CAN=180°,
∴∠AFC=∠B+∠CAN=45°+∠CAN,
∵∠FAC=∠FAP+∠PAC=45°+∠PAC,
∴∠FAC=∠AFC,
∴∠CAN=∠PAC,
∵∠APC=∠FPC=![]() =135°=∠ANC,
=135°=∠ANC,
∴△APC≌△ANC(AAS),
∴AP=AN,
∵AM=AN+MN,
∴![]() AM=
AM=![]() AN+
AN+![]() MN=AF+CD=AF+AB,
MN=AF+CD=AF+AB,
即AF+AB=![]() AM.
AM.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
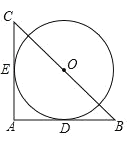
【题目】如图,在 Rt△ABC 中BC=2![]() ,以 BC 的中点 O 为圆心的⊙O 分别与 AB,AC 相切于 D,E 两点,
,以 BC 的中点 O 为圆心的⊙O 分别与 AB,AC 相切于 D,E 两点,![]() 的长为( )
的长为( )
A.![]() B.
B.![]() C.πD.2π
C.πD.2π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在等边△ABC中,点D是边AC上一点,连接BD,将△BCD绕着点B逆时针旋转60,得到△BAE,连接ED,则下列结论中:①AE∥BC;②∠DEB=60;③∠ADE=∠BDC,其中正确结论的序号是( )
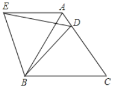
A.①②B.①③C.②③D.只有①
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一、阅读材料:
已知实数m,n满足(2m2+n2+1)(2m2+n2-1)=80,试求2m2+n2的值.
解:设2m2+n2=t,则原方程变为(t+1)(t-1)=80,整理得t2-1=80,t2=81,所以t=土9,因为2m2+n2>0,所以2m2+n2=9.
二、方法归纳:
上面这种方法称为“ 法”,把其中某些部分看成一个整体,并用新字母代替(即换元),则能使复杂的问题简单化.
三、探索实践:
根据以上阅读材料内容,解决下列问题,并写出解答过程.
(1)已知实数x、y,满足(2x2+2y2+3)(2x2+2y2-3)=27,求x2+y2的值.
(2)已知Rt△ACB的三边为a、b、c(c为斜边),其中a、b满足(a2+b2)(a2+b2-4)=5,求Rt△ACB外接圆的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+2x+c经过点A(0,3),B(-1,0),请回答下列问题:
(1)求抛物线对应的二次函数的表达式;
(2)抛物线的顶点为D,对称轴与x轴交于点E,连接BD,求BD的长.
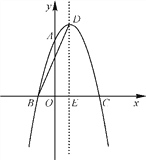
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】)甲乙两人在相同条件下完成了5次射击训练,两人的成绩如图所示.

(1)甲射击成绩的众数为 环,乙射击成绩的中位数为 环;
(2)计算两人射击成绩的方差;
(3)根据训练成绩,你认为选派哪一名队员参赛更好,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E是AD边的中点,BD,CE交于点H,BE、AH交于点G,则下列结论:①∠ABE=∠DCE;②AG⊥BE;③S△BHE=S△CHD;④∠AHB=∠EHD.其中正确的是( )
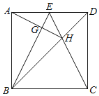
A.①③B.①②③④C.①②③D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在甲乙两个不透明的口袋中,分别有大小、材质完全相同的小球,其中甲口袋中的小球上分别标有数字1,2,3,4,乙口袋中的小球上分别标有数字2,3,4,先从甲袋中任意摸出一个小球,记下数字为m,再从乙袋中摸出一个小球,记下数字为n.
(1)请用列表或画树状图的方法表示出所有(m,n)可能的结果;
(2)若m,n都是方程x2﹣5x+6=0的解时,则小明获胜;若m,n都不是方程x2﹣5x+6=0的解时,则小利获胜,问他们两人谁获胜的概率大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=-x2+mx+n与x轴交于点A,B(A在B的左侧).
(1)抛物线的对称轴为直线x=-3,AB=4.求抛物线的表达式;
(2)平移(1)中的抛物线,使平移后的抛物线经过点O,且与x正半轴交于点C,记平移后的抛物线顶点为P,若△OCP是等腰直角三角形,求点P的坐标;
(3)当m=4时,抛物线上有两点M(x1,y1)和N(x2,y2),若x1<2,x2>2,x1+x2>4,试判断y1与y2的大小,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com