
【题目】如图,已知一次函数与反比例函数的图象交于点A(﹣4,﹣2)和B(a,4).
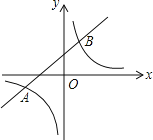
(1)求一次函数和反比例函数的表达式及点B的坐标;
(2)根据图象回答,当x在什么范围内时,一次函数的值大于反比例函数.
【答案】(1)一次函数表达式为y=x+2;反比例函数的解析式为y=![]() .点B的坐标为B(2,4);(2)当x>2或﹣4<x<0时,一次函数的值大于反比例函数的值.
.点B的坐标为B(2,4);(2)当x>2或﹣4<x<0时,一次函数的值大于反比例函数的值.
【解析】
试题分析:(1)设反比例函数的解析式为y=![]() (k≠0),把A点坐标代入即可得出k的值,进而得出反比例函数的解析式,再把B点坐标代入即可得出a的值,利用待定系数法即可得出一次函数的解析式;
(k≠0),把A点坐标代入即可得出k的值,进而得出反比例函数的解析式,再把B点坐标代入即可得出a的值,利用待定系数法即可得出一次函数的解析式;
(2)直接根据两函数的交点即可得出结论.
解:(1)设反比例函数的解析式为y=![]() (k≠0),
(k≠0),
∵反比例函数图象经过点A(﹣4,﹣2),
∴﹣2=![]() ,解得k=8,
,解得k=8,
∴反比例函数的解析式为y=![]() .
.
∵B(a,4)在y=![]() 的图象上,
的图象上,
∴4=![]() ,
,
∴a=2,
∴点B的坐标为B(2,4);
设一次函数表达式为y=mx+n,将点A,点B代入得,![]() ,解得
,解得![]() ,
,
∴一次函数表达式为y=x+2;
(2)根据图象得,当x>2或﹣4<x<0时,一次函数的值大于反比例函数的值.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知抛物线y=﹣![]() +c与x轴交于A、B两点(点A在点B的左侧),交y轴的正半轴于点C,其顶点为M,MH⊥x轴于点H,MA交y轴于点N,sin∠MOH=
+c与x轴交于A、B两点(点A在点B的左侧),交y轴的正半轴于点C,其顶点为M,MH⊥x轴于点H,MA交y轴于点N,sin∠MOH=![]() .
.
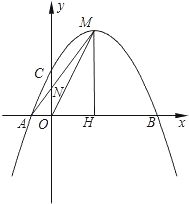
(1)求此抛物线的函数表达式;
(2)过H的直线与y轴相交于点P,过O,M两点作直线PH的垂线,垂足分别为E,F,若![]() =
=![]() 时,求点P的坐标;
时,求点P的坐标;
(3)将(1)中的抛物线沿y轴折叠,使点A落在点D处,连接MD,Q为(1)中的抛物线上的一动点,直线NQ交x轴于点G,当Q点在抛物线上运动时,是否存在点Q,使△ANG与△ADM相似?若存在,求出所有符合条件的直线QG的解析式;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超市有一种“喜之郎”果冻礼盒,内装两个上下倒置的果冻,果冻高为4cm,底面是个直径为6cm的圆,横截面可以近似地看作一个抛物线,为了节省成本,包装应尽可能的小,那么要制作这样一个包装盒至少纸板( )平方厘米.(不计重合部分)
A.253 B.288 C.206 D.245
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我省2013年的快递业务量为1.4亿件,受益于电子商务发展和法治环境改善等多重因素,快递业务迅猛发展,2014年增速位居全国第一.若2015年的快递业务量达到4.5亿件,设2014年与2015年这两年的平均增长率为x,则下列方程正确的是( )
A. 1.4(1+x)=4.5 B. 1.4(1+2x)=4.5
C. 1.4(1+x)2=4.5 D. 1.4(1+x)+1.4(1+x)2=4.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com