
【题目】在平面直角坐标系xOy中,已知抛物线y=﹣![]() +c与x轴交于A、B两点(点A在点B的左侧),交y轴的正半轴于点C,其顶点为M,MH⊥x轴于点H,MA交y轴于点N,sin∠MOH=
+c与x轴交于A、B两点(点A在点B的左侧),交y轴的正半轴于点C,其顶点为M,MH⊥x轴于点H,MA交y轴于点N,sin∠MOH=![]() .
.
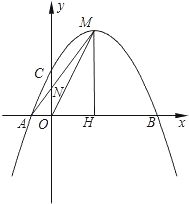
(1)求此抛物线的函数表达式;
(2)过H的直线与y轴相交于点P,过O,M两点作直线PH的垂线,垂足分别为E,F,若![]() =
=![]() 时,求点P的坐标;
时,求点P的坐标;
(3)将(1)中的抛物线沿y轴折叠,使点A落在点D处,连接MD,Q为(1)中的抛物线上的一动点,直线NQ交x轴于点G,当Q点在抛物线上运动时,是否存在点Q,使△ANG与△ADM相似?若存在,求出所有符合条件的直线QG的解析式;若不存在,请说明理由.
【答案】(1)y=﹣![]() +4;(2)P(0,2)或P(0,﹣2).(3)存在,符合条件的所有直线QG的解析式为:y=4x+
+4;(2)P(0,2)或P(0,﹣2).(3)存在,符合条件的所有直线QG的解析式为:y=4x+![]() 或y=﹣
或y=﹣![]() x+
x+![]() .
.
【解析】
试题分析:(1)由抛物线y=﹣![]() +c与x轴交于A、B两点(点A在点B的左侧),交y轴的正半轴于点C,其顶点为M,MH⊥x轴于点H,MA交y轴于点N,sin∠MOH=
+c与x轴交于A、B两点(点A在点B的左侧),交y轴的正半轴于点C,其顶点为M,MH⊥x轴于点H,MA交y轴于点N,sin∠MOH=![]() ,求出c的值,进而求出抛物线方程;
,求出c的值,进而求出抛物线方程;
(2)如图1,由OE⊥PH,MF⊥PH,MH⊥OH,可证△OEH∽△HFM,可知HE,HF的比例关系,求出P点坐标;
(3)首先求出D点坐标,写出直线MD的表达式,由两直线平行,两三角形相似,可得NG∥MD,直线QG解析式.
解:(1)∵M为抛物线y=﹣![]() +c的顶点,
+c的顶点,
∴M(2,c).
∴OH=2,MH=|c|.
∵a<0,且抛物线与x轴有交点,
∴c>0,
∴MH=c,
∵sin∠MOH=![]() ,
,
∴![]() =
=![]() .
.
∴OM=![]() c,
c,
∵OM2=OH2+MH2,
∴MH=c=4,
∴M(2,4),
∴抛物线的函数表达式为:y=﹣![]() +4.
+4.
(2)如图1,∵OE⊥PH,MF⊥PH,MH⊥OH,
∴∠EHO=∠FMH,∠OEH=∠HFM.
∴△OEH∽△HFM,
∴![]() =
=![]() =
=![]() ,
,
∵![]() =
=![]() ,
,
∴MF=HF,
∴∠OHP=∠FHM=45°,
∴OP=OH=2,
∴P(0,2).
如图2,同理可得,P(0,﹣2).
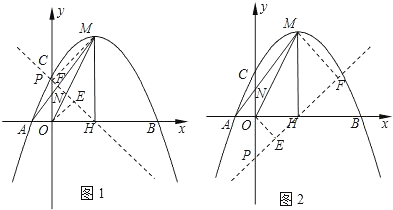
(3)∵A(﹣1,0),
∴D(1,0),
∵M(2,4),D(1,0),
∴直线MD解析式:y=4x﹣4,
∵ON∥MH,∴△AON∽△AHM,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
∴AN=![]() ,ON=
,ON=![]() ,N(0,
,N(0,![]() ).
).
如图3,若△ANG∽△AMD,可得NG∥MD,
∴直线QG解析式:y=4x+![]() ,
,
如图4,若△ANG∽△ADM,可得![]() =
=![]()
∴AG=![]() ,
,
∴G(![]() ,0),
,0),
∴QG:y=﹣![]() x+
x+![]() ,
,
综上所述,符合条件的所有直线QG的解析式为:y=4x+![]() 或y=﹣
或y=﹣![]() x+
x+![]() .
.
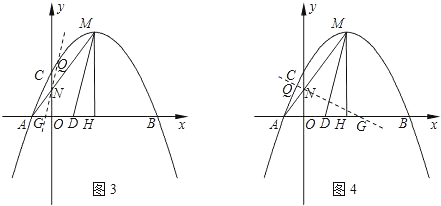


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】时代超市出售的三种品牌月饼袋上,分别标有质量为:(500±5)g、(500±10)g、(500±20)g的字样,从中任意拿出两袋,它们的质量最多相差( )
A.10g
B.20g
C.30g
D.40g
查看答案和解析>>
科目:初中数学 来源: 题型:
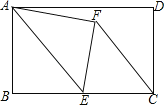
【题目】如图,在矩形ABCD中,AB=8,BC=12,点E是BC的中点,连接AE,将△ABE沿AE折叠,点B落在点F处,连接FC,则tan∠ECF=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2013年1月1日新交通法规开始实施.为了解某社区居民遵守交通法规情况,小明随机选取部分居民就“行人闯红灯现象”进行问卷调查,调查分为“A:从不闯红灯;B:偶尔闯红灯;C:经常闯红灯;D:其他”四种情况,并根据调查结果绘制出部分条形统计图(如图1)和部分扇形统计图(如图2).请根据图中信息,解答下列问题:
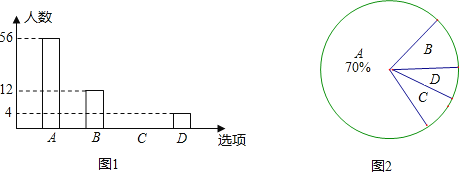
(1)本次调查共选取名居民;
(2)求出扇形统计图中“C”所对扇形的圆心角的度数,并将条形统计图补充完整;
(3)如果该社区共有居民1600人,估计有多少人从不闯红灯?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种袋装大米的质量标识为“10±0.25千克”,则下列几袋大米中合格的是( )
A. 9.70千克 B. 10.30千克 C. 10.51千克 D. 9.80千克
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数与反比例函数的图象交于点A(﹣4,﹣2)和B(a,4).
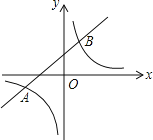
(1)求一次函数和反比例函数的表达式及点B的坐标;
(2)根据图象回答,当x在什么范围内时,一次函数的值大于反比例函数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题背景】
(1)如图1的图形我们把它称为“8字形”,请说明![]() ;
;

【简单应用】
(2)阅读下面的内容,并解决后面的问题:如图2, AP、CP分别平分∠BAD. ∠BCD,若∠ABC=36°,∠ADC=16°,求∠P的度数;

解:∵AP、CP分别平分∠BAD. ∠BCD
∴∠1=∠2,∠3=∠4
由(1)的结论得: ![]()
①+②,得2∠P+∠2+∠3=∠1+∠4+∠B+∠D
∴∠P =![]() (∠B+∠D)=26°.
(∠B+∠D)=26°.
【问题探究】如图3,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,若∠ABC=36°,∠ADC=16°,请猜想![]() 的度数,并说明理由.
的度数,并说明理由.

【拓展延伸】
① 在图4中,若设∠C=α,∠B=β,∠CAP=![]() ∠CAB,∠CDP=
∠CAB,∠CDP=![]() ∠CDB,试问∠P与∠C、∠B之间的数量关系为:________________(用α、β表示∠P),
∠CDB,试问∠P与∠C、∠B之间的数量关系为:________________(用α、β表示∠P),

②在图5中,AP平分∠BAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的关系,直接写出结论______________________
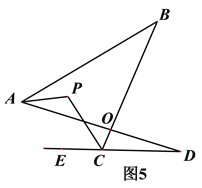
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com