
【题目】阅读下列推理过程,将空白部分补充完整.
(1)如图1,∠ABC=∠A1B1C1,BD,B1D1分别是∠ABC,∠A1B1C1的角平分线,对∠DBC=∠D1B1C1进行说理.
理由:因为BD,B1D1分别是∠ABC,∠A1B1C1的角平分线
所以∠DBC= ,∠D1B1C1= (角平分线的定义)
又因为∠ABC=∠A1B1C1
所以![]() ∠ABC=
∠ABC=![]() ∠A1B1C1
∠A1B1C1
所以∠DBC=∠D1B1C1( )

(2)如图2,EF∥AD,∠1=∠2,∠B=40°,求∠CDG的度数.
因为EF∥AD,
所以∠2= ( )
又因为∠1=∠2 (已知)
所以∠1= (等量代换)
所以AB∥GD( )
所以∠B= ( )
因为∠B=40°(已知)
所以∠CDG= (等量代换)
(3)下面是“积的乘方的法则“的推导过程,在括号里写出每一步的依据.
因为(ab)n=![]() ( )
( )
=![]() ( )
( )
=anbn( )
所以(ab)n=anbn.
【答案】(1)∠ABC,∠A1B1C1,等量代换(2)∠3,两直线平行,同位角相等,∠3,内错角相等,两直线平行,∠CDG,两直线平行,同位角相等,40°(3)乘方的意义,乘法交换律、乘法结合律,乘方的意义
【解析】
(1)根据角平分线定义求出即可;
(2)根据平行线的性质和已知求出∠1=∠3,根据平行线的判定推出DG∥AB,根据平行线的性质得出即可;
(3)根据乘方的意义和乘法运算律求出即可.
(1)理由是:∵BD,B1D1分别是∠ABC,∠A1B1C1的角平分线,∴∠DBC=![]() ,∠D1B1C1=
,∠D1B1C1=![]() ∠A1B1C1(角平分线的定义).
∠A1B1C1(角平分线的定义).
又因为∠ABC=∠A1B1C1,所以![]() ∠ABC=
∠ABC=![]() ∠A1B1C1,所以∠DBC=∠D1B1C1(等量代换).
∠A1B1C1,所以∠DBC=∠D1B1C1(等量代换).
故答案为:∠ABC,∠A1B1C1,等量代换;
(2)∵EF∥AD,∴∠2=∠3(两直线平行,同位角相等).
又∵∠1=∠2 (已知),所以∠1=∠3(等量代换),∴AB∥GD(内错角相等,两直线平行),∴∠B=∠CDG(两直线平行,同位角相等).
∵∠B=40°(已知),∴∠CDG=40°(等量代换).
故答案为:∠3,两直线平行,同位角相等,∠3,内错角相等,两直线平行,∠CDG,两直线平行,同位角相等,40°;
(3)∵(ab)n=![]() (乘方的意义)
(乘方的意义)
=![]() (乘法交换律、乘法结合律)
(乘法交换律、乘法结合律)
=anbn(乘方的意义)
∴(ab)n=anbn.


科目:初中数学 来源: 题型:
【题目】为发展校园足球运动,某县城区四校决定联合购买一批足球运动装备,市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球;乙商场优惠方案是:若购买队服超过80套,则购买足球打八折.
(1)求每套队服和每个足球的价格是多少?
(2)若城区四校联合购买100套队服和a个足球,请用含a的式子分别表示出到甲商场和乙商场购买装备所花的费用;
(3)假如你是本次购买任务的负责人,你认为到哪家商场购买比较合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果∠A和∠B互补,且∠A>∠B,给出下列四个式子:①90°﹣∠B;②∠A﹣90°;③![]() (∠A+∠B)④
(∠A+∠B)④![]() (∠A﹣∠B)其中表示∠B余角的式子有_____.(填序号)
(∠A﹣∠B)其中表示∠B余角的式子有_____.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班将举行“数学知识竞赛”活动,班长安排小明购买奖品,下面两图是小明买回奖品时与班长的对话情境:

请根据上面的信息,解决问题:
(1)试计算两种笔记本各买了多少本?
(2)请你解释:小明为什么不可能找回68元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假期间,两名教师计划带领若干名学生去旅游,他们联系了报价均为每人500元的两家旅行社![]() 经协商,甲旅行社的优惠条件是:两名教师全额收费,学生都按七折收费;乙旅行社的优惠条件是:教师、学生都按八折收费
经协商,甲旅行社的优惠条件是:两名教师全额收费,学生都按七折收费;乙旅行社的优惠条件是:教师、学生都按八折收费![]() 请你帮他们选择一下,选哪家旅行社比较合算.
请你帮他们选择一下,选哪家旅行社比较合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,且与y轴交于点C,点D是抛物线的顶点,抛物线的对称轴DE交x轴于点E,连接BD.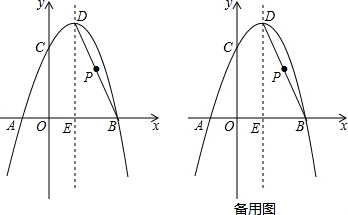
(1)求经过A,B,C三点的抛物线的函数表达式;
(2)点P是线段BD上一点,当PE=PC时,求点P的坐标;
(3)在(2)的条件下,过点P作PF⊥x轴于点F,G为抛物线上一动点,M为x轴上一动点,N为直线PF上一动点,当以F、M、N、G为顶点的四边形是正方形时,请求出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠A=120°,∠C=80°.将△BMN沿着MN翻折,得到△FMN.若MF∥AD,FN∥DC,则∠F的度数为( )
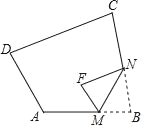
A. 70° B. 80° C. 90° D. 100°
查看答案和解析>>
科目:初中数学 来源: 题型:
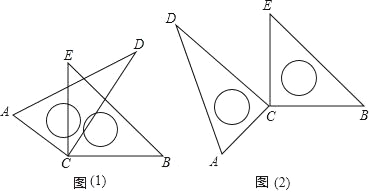
【题目】数学活动课上,小聪同学摆弄着自己刚购买的一套三角板,将两块直角三角板的直角顶点C叠放在一起,然后转动三角板,在转动过程中,请解决以下问题:
(1)如图(1):当∠DCE=30°时,∠ACB+∠DCE= ,若∠DCE为任意锐角时,你还能求出∠ACB与∠DCE的数量关系吗?若能,请求出;若不能,请说明理由.
(2)当转动到图(2)情况时,∠ACB与∠DCE有怎样的数量关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有甲、乙两个容器,分别装有进水管和出水管,两容器的进、出水速度不变,先打开乙容器的进水管,2分钟时再打开甲容器的进水管,又过2分钟关闭甲容器的进水管,再过4分钟同时打开甲容器的进、出水管.直到12分钟时,同时关闭两容器的进、出水管.打开和关闭水管的时间忽略不计.容器中的水量y(升)与乙容器注水时间x(分)之间的关系如图所示.
(1)求甲容器的进、出水速度;
(2)甲容器的进、出水管都关闭后,是否存在两容器的水量相等?若存在,求出此时的时间.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com