
����Ŀ����ͼ��������y=��x2+bx+c����A����1��0����B��3��0�����㣬����y�ύ�ڵ�C����D�������ߵĶ��㣬�����ߵĶԳ���DE��x���ڵ�E������BD��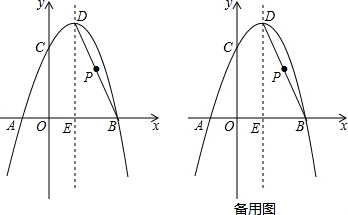
��1����A��B��C����������ߵĺ�������ʽ��
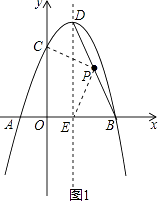
��2����P���߶�BD��һ�㣬��PE=PCʱ�����P�����ꣻ
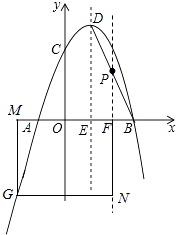
��3���ڣ�2���������£�����P��PF��x���ڵ�F��GΪ��������һ���㣬MΪx����һ���㣬NΪֱ��PF��һ���㣬����F��M��N��GΪ������ı�����������ʱ���������M�����꣮
���𰸡�
��1��
�⣺��������y=��x2+bx+c����A����1��0����B��3��0�����㣬
�� ![]() ��
��
��ã� ![]() ��
��
�ྭ��A��B��C����������ߵĺ�������ʽΪy=��x2+2x+3
��2��
�⣺��ͼ1������PC��PE��
x=�� ![]() =��
=�� ![]() =1��
=1��
��x=1ʱ��y=4��
���D��������1��4����
��ֱ��BD�Ľ���ʽΪ��y=mx+n��
�� ![]() ��
��
��ã� ![]() ��
��
��ֱ��BD�Ľ���ʽΪy=��2x+6��
���P��������x����2x+6����
��PC2=x2+��3+2x��6��2��PE2=��x��1��2+����2x+6��2��
��PC=PE��
��x2+��3+2x��6��2=��x��1��2+����2x+6��2��
��ã�x=2��
��y=��2��2+6=2��
���P��������2��2��
��3��
�⣺���M������Ϊ��a��0�������G������Ϊ��a����a2+2a+3����
����F��M��N��GΪ������ı����������Σ�
��FM=MG����|2��a|=|��a2+2a+3|��
��2��a=��a2+2a+3ʱ��
�����ã�a2��3a��1=0��
��ã�a= ![]() ��
��
��2��a=������a2+2a+3��ʱ��
�����ã�a2��a��5=0��
��ã�a= ![]() ��
��
�൱��F��M��N��GΪ������ı�����������ʱ����M������Ϊ�� ![]() ��0������
��0������ ![]() ��0������
��0������ ![]() ��0������
��0������ ![]() ��0��
��0��
����������1�����ô���ϵ���������A��B��C����������ߵĺ�������ʽ����2������PC��PE�����ù�ʽ�������D�����꣬���ô���ϵ�������ֱ��BD�Ľ���ʽ�������P������Ϊ��x����2x+6�������ù��ɶ�����ʾ��PC2��PE2 �� ���������г����̣��ⷽ�����x��ֵ�����������P�����ꣻ��3�����M������Ϊ��a��0������ʾ����G�����꣬���������ε������г����̣��ⷽ�̼��ɣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֲ��������֮�ʣ�ѧУ������һ�����磬��֪2�ü��������5���������繲��113Ԫ��3�ü��������2���������繲��87Ԫ��
��1����һ�ü��������һ������������ۼ۸��Ƕ���Ԫ��
��2��ѧУ���������������繲100�ã�����������������������ڼ�������������2��������Ƴ���ʡǮ�Ĺ������������ʱ���ܷ��ã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ(1)��AB��4cm��AC��AB��BD��AB��AC��BD��3cm����P���߶�AB����1cm/s���ٶ��ɵ�A���B�˶���ͬʱ����Q���߶�BD���ɵ�B���D�˶��������˶���ʱ��Ϊt(s)��
(1)����Q���˶��ٶ����P���˶��ٶ���ȣ���t��1ʱ����ACP���BPQ�Ƿ�ȫ�ȣ���˵�����ɣ����жϴ�ʱ�߶�PC���߶�PQ��λ�ù�ϵ��
(2)��ͼ(2)����ͼ(1)�еġ�AC��AB��BD��AB��Ϊ�ġ���CAB����DBA��60�㡱�������������䣮���Q���˶��ٶ�Ϊx cm/s���Ƿ����ʵ��x��ʹ�á�ACP���BPQȫ�ȣ������ڣ������Ӧ��x��t��ֵ���������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У���E��F�ֱ��ڱ�AB��BC�ϣ���AE=![]() AB����������ֱ��EF�۵�����Bǡ������AD���ϵĵ�P��������BP��EF�ڵ�Q���������н��ۣ���EF=2BE����PF=2PE����FQ=4EQ���ܡ�PBF�ǵȱ������Σ�������ȷ���ǣ� ��
AB����������ֱ��EF�۵�����Bǡ������AD���ϵĵ�P��������BP��EF�ڵ�Q���������н��ۣ���EF=2BE����PF=2PE����FQ=4EQ���ܡ�PBF�ǵȱ������Σ�������ȷ���ǣ� ��

A. �٢� B. �ڢ� C. �٢� D. �٢�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ������������̣����հײ��ֲ���������
��1����ͼ1����ABC=��A1B1C1��BD��B1D1�ֱ�����ABC����A1B1C1�Ľ�ƽ���ߣ�����DBC=��D1B1C1����˵����
���ɣ���ΪBD��B1D1�ֱ�����ABC����A1B1C1�Ľ�ƽ����
������DBC=�� ������D1B1C1=�� ������ƽ���ߵĶ��壩
������ABC=��A1B1C1
����![]() ��ABC=
��ABC=![]() ��A1B1C1
��A1B1C1
������DBC=��D1B1C1���� ����

��2����ͼ2��EF��AD����1=��2����B=40�㣬����CDG�Ķ�����
��ΪEF��AD��
������2=�� ������ ����
����Ϊ��1=��2 ����֪��
������1=�� ��������������
����AB��GD���� ����
������B=�� ������ ����
��Ϊ��B=40�㣨��֪��
������CDG=�� ��������������
��3�������������ij˷��ķ����Ƶ����̣���������д��ÿһ�������ݣ�
����ab��n=![]() ���� ����
���� ����
=![]() ���� ����
���� ����
=anbn���� ����
���ԣ�ab��n=anbn��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����AOB��ֱ�������Σ���AOB=90�㣬OB=2OA����A�ڷ���������y= ![]() ��ͼ���ϣ�����B�ڷ���������y=
��ͼ���ϣ�����B�ڷ���������y= ![]() ��ͼ���ϣ���k��ֵΪ ��
��ͼ���ϣ���k��ֵΪ �� 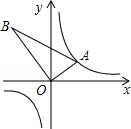
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC����ABΪֱ���ġ�O�ֱ���BC��AC���ڵ�D��E������D����O������DF����AC�ڵ�F�� 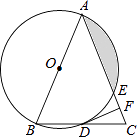
��1����֤��DF��AC��
��2������O�İ뾶Ϊ4����CDF=22.5�㣬����Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�OA��OB��AB��x���ڵ�C����A�� ![]() ��1���ڷ���������y=
��1���ڷ���������y= ![]() ��ͼ���ϣ�
��ͼ���ϣ�
��1����������y= ![]() �ı���ʽ��
�ı���ʽ��
��2����x��ĸ������ϴ���һ��P��ʹ��S��AOP= ![]() S��AOB �� ���P�����ꣻ
S��AOB �� ���P�����ꣻ
��3��������BOA�Ƶ�B����ʱ�뷽����ת60��õ���BDE��ֱ��д����E�����꣬���жϵ�E�Ƿ��ڸ÷�����������ͼ���ϣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com