
【题目】数学活动课上,小聪同学摆弄着自己刚购买的一套三角板,将两块直角三角板的直角顶点C叠放在一起,然后转动三角板,在转动过程中,请解决以下问题:
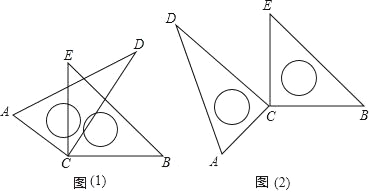
(1)如图(1):当∠DCE=30°时,∠ACB+∠DCE= ,若∠DCE为任意锐角时,你还能求出∠ACB与∠DCE的数量关系吗?若能,请求出;若不能,请说明理由.
(2)当转动到图(2)情况时,∠ACB与∠DCE有怎样的数量关系?请说明理由.
【答案】(1)∠ACB+∠DCE=180°(2)∠ACB+∠DCE=180°
【解析】
(1)当∠DCE=30°时,利用互余计算出∠BCD,然后可得到∠ACB+∠DCE的度数;若∠DCE为任意锐角时,利用∠ACE+∠DCE=90°,∠BCD+∠DCE=90°,然后计算出∠ACB+∠DCE=180°;
(2)利用周角定义得到∠ACD+∠ECB+∠ACB+∠DCE=360°,所以∠ECD+∠ACB=360°﹣(∠ACD+∠ECB)=180°.
(1)∠ACB+∠DCE=180°;若∠DCE为任意锐角时,∠ACB+∠DCE=180°.理由如下:
∵∠ACE+∠DCE=90°,∠BCD+∠DCE=90°,∴∠ACB+∠DCE=∠ACE+∠DCE+∠BCD+∠DCE=90°+90°=180°;
(2)∠ACB+∠DCE=180°.理由如下:
∵∠ACD=90°=∠ECB,∠ACD+∠ECB+∠ACB+∠DCE=360°,∴∠ECD+∠ACB=360°﹣(∠ACD+∠ECB)=360°﹣180°=180°.


科目:初中数学 来源: 题型:
【题目】如图,大树AB与大数CD相距13m,小华从点B沿BC走向点C,行走一段时间后他到达点E,此时他仰望两棵大树的顶点A和D,两条视线的夹角正好为90°,且EA=ED.已知大树AB的高为5m,小华行走的速度为1m/s,小华行走到点E的时间是( )

A. 13s B. 8s C. 6s D. 5s
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列推理过程,将空白部分补充完整.
(1)如图1,∠ABC=∠A1B1C1,BD,B1D1分别是∠ABC,∠A1B1C1的角平分线,对∠DBC=∠D1B1C1进行说理.
理由:因为BD,B1D1分别是∠ABC,∠A1B1C1的角平分线
所以∠DBC= ,∠D1B1C1= (角平分线的定义)
又因为∠ABC=∠A1B1C1
所以![]() ∠ABC=
∠ABC=![]() ∠A1B1C1
∠A1B1C1
所以∠DBC=∠D1B1C1( )

(2)如图2,EF∥AD,∠1=∠2,∠B=40°,求∠CDG的度数.
因为EF∥AD,
所以∠2= ( )
又因为∠1=∠2 (已知)
所以∠1= (等量代换)
所以AB∥GD( )
所以∠B= ( )
因为∠B=40°(已知)
所以∠CDG= (等量代换)
(3)下面是“积的乘方的法则“的推导过程,在括号里写出每一步的依据.
因为(ab)n=![]() ( )
( )
=![]() ( )
( )
=anbn( )
所以(ab)n=anbn.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y= ![]() 的图象上.若点B在反比例函数y=
的图象上.若点B在反比例函数y= ![]() 的图象上,则k的值为 .
的图象上,则k的值为 . 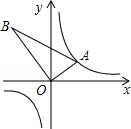
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F. 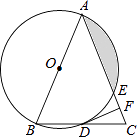
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD的对角线AC、BD的长分别为10厘米、6厘米,且AC与BD互相垂直,顺次连接四边形ABCD四边的中点E、F、G、H得四边形EFGH,则四边形EFGH的面积为_____平方厘米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有三个点A、B、C,完成下列问题:
![]()
(1)将点B向右移动六个单位长度到点D,在数轴上表示出点D.
(2)在数轴上找到点E,使点E为BA的中点(E到A、C两点的距离相等),井在数轴上标出点E表示的数,求出CE的长.
(3)O为原点,取OC的中点M,分OC分为两段,记为第一次操作:取这两段OM、CM的中点分别为了N1、N2,将OC分为4段,记为第二次操作,再取这两段的中点将OC分为8段,记为第三次操作,第六次操作后,OC之间共有多少个点?求出这些点所表示的数的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于有理数a、b,定义运算:a![]() b=a×b-a-b+1.
b=a×b-a-b+1.
(1)计算5![]() (-2)与(-2)
(-2)与(-2)![]() 5的值,并猜想a
5的值,并猜想a![]() b与b
b与b![]() a的大小关系;
a的大小关系;
(2)求(-3)![]() [4
[4![]() (-2)]的值.
(-2)]的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com