练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】对于有理数a、b，定义运算：ab=a×b-a-b+1．

    （1）计算5（-2）与（-2）5的值，并猜想ab与ba的大小关系；

    （2）求（-3） [4（-2）]的值．

    【答案】(1) ab＝ba；(2)40.

    【解析】

    (1)先按新定义运算,相等,按新定义分别运算即可说明理由;
    (2)按照定义得运算规则先计算括号内的即可.

    解：（1）5（2）＝5×（2）5（2）＋1＝105＋2＋1＝12，

    （2）5＝（2）×5（2）5＋1＝10＋25＋1＝12，

    猜想：ab＝ba，

    ∵ab＝a×bab＋1，ba＝b×aba＋1；

    ∴ab＝ba；

    （2）（3） [4（2）]

    ＝（3） [4×（2）4（2）＋1]

    ＝（3）（84＋2＋1）

    ＝（3）（9）

    ＝3×（9）（3）（9）＋1

    ＝27＋3＋9＋1

    ＝40．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

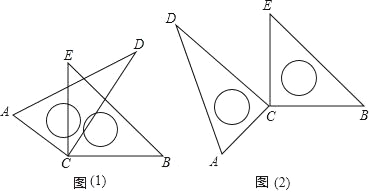
    【题目】数学活动课上，小聪同学摆弄着自己刚购买的一套三角板，将两块直角三角板的直角顶点C叠放在一起，然后转动三角板，在转动过程中，请解决以下问题：

    （1）如图（1）：当∠DCE=30°时，∠ACB+∠DCE=　 　，若∠DCE为任意锐角时，你还能求出∠ACB与∠DCE的数量关系吗？若能，请求出；若不能，请说明理由．

    （2）当转动到图（2）情况时，∠ACB与∠DCE有怎样的数量关系？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】现有甲、乙两个容器,分别装有进水管和出水管,两容器的进、出水速度不变,先打开乙容器的进水管,2分钟时再打开甲容器的进水管,又过2分钟关闭甲容器的进水管,再过4分钟同时打开甲容器的进、出水管.直到12分钟时,同时关闭两容器的进、出水管.打开和关闭水管的时间忽略不计.容器中的水量y(升)与乙容器注水时间x(分)之间的关系如图所示.

    (1)求甲容器的进、出水速度;

    (2)甲容器的进、出水管都关闭后,是否存在两容器的水量相等?若存在,求出此时的时间.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商场用2730元购进A、B两种新型节能日光灯共60盏，这两种日光灯的进价、标价如下表所示．

    价格/类型

    A型

    B型

    进价（元/盏）

    35

    65

    标价（元/盏）

    50

    100

    （1）这两种日光灯各购进多少盏？

    （2）若A型日光灯按标价的9折出售，要使这批日光灯全部售出后商场获得810元的利润，则B型日光灯应按标价的几折出售？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

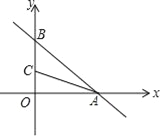
    【题目】在平面直角坐标系中，已知一次函数y=﹣x+6与x，y轴分别交于A，B两点，点C（0，n）是y轴上一点，把坐标平面沿直线AC折叠，点B刚好落在x轴上，则点C的坐标是（　　）

    A. （0，3） B. （0，） C. （0，） D. （0，）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在直角坐标系中将下列各点用线段依次连结起来，能得到什么图案？

    (0，0)，(－4，－2)，(－3，0)，(－5，－1)，(－5，1)，(－3，0)，(－4，2)，(0，0)．

    (1)若以上各点纵坐标保持不变，横坐标分别加3，再将所得的点用线段依次连结起来，所得的图案与原来的图案相比有什么变化？若横坐标不变，纵坐标分别加3呢？

    (2)连结点(3，3)，(－1，1)，(0，3)，(－2，2)，(－2，4)，(0，3)，(－1，5)，(3，3)，观察所得图案和原图案的位置关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形ABCD中，AB=4，AD=5，AD、AB、BC分别与⊙O相切于E、F、G三点，过点D作⊙O的切线交BC于点M，切点为N，则DM的长为（ ）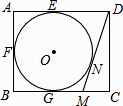
    A.
    B.2
    C.
    D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】先阅读下面一段文字，再回答后面的问题．

    已知在平面直角坐标系内两点P1(x1，y1)，P2(x2，y2)，点P1，P2间的距离公式P1P2＝，同时，当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时，两点间的距离公式可简化为|x2－x1|或|y2－y1|.

    (1)已知A(2，4)，B(－3，－8)，试求A，B两点间的距离；

    (2)已知各顶点坐标为A(0，6)，B(－3，2)，C(3，2)，你能判定△ABC的形状吗？并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在边长为1的正方形网格中标有A、B、C、D、E、F六个格点，根据图中标示的各点位置，与△ABC全等的是（　　）

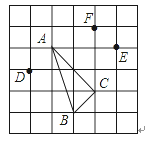
    A. △ACF B. △ACE C. △ABD D. △CEF

    查看答案和解析>>

    同步练习册答案