
【题目】在直角坐标系中将下列各点用线段依次连结起来,能得到什么图案?
(0,0),(-4,-2),(-3,0),(-5,-1),(-5,1),(-3,0),(-4,2),(0,0).
(1)若以上各点纵坐标保持不变,横坐标分别加3,再将所得的点用线段依次连结起来,所得的图案与原来的图案相比有什么变化?若横坐标不变,纵坐标分别加3呢?
(2)连结点(3,3),(-1,1),(0,3),(-2,2),(-2,4),(0,3),(-1,5),(3,3),观察所得图案和原图案的位置关系.
【答案】(1)见解析;(2)见解析.
【解析】
(1)作出平面直角坐标系并描出各点然后连接,再根据平移的性质解答即可;
(2)在平面直角坐标系中找出各点的位置,然后解答即可.
将(0,0),(-4,-2),(-3,0),(-5,-1),(-5,1),(-3,0),(-4,2),(0,0)各点用线段依次连结起来,如图①,得到的图案是条鱼.
(1)若纵坐标保持不变,横坐标分别加3,得到的坐标分别是(3,0),(-1,-2),(0,0),(-2,-1),(-2,1),(0,0),(-1,2),(3,0),用线段依次连结起来,如图②,所得的图案依然是一条鱼,与原来的图案相比,形状、大小不变,只是向右平移了3个单位;若横坐标不变,纵坐标分别加3,得到的坐标分别是(0,3),(-4,1),(-3,3),(-5,2),(-5,4),(-3,3),(-4,5),(0,3),用线段依次连结起来,如图③,与原来的图案相比,形状、大小不变,只是向上平移了3个单位.
(2)连结点(3,3),(-1,1),(0,3),(-2,2),(-2,4),(0,3),(-1,5),(3,3),如图④,由观察可知此图案是由原图案先向上平移了3个单位,再向右平移了3个单位得到的.
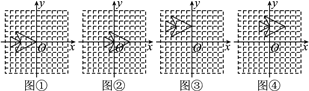


 高效智能课时作业系列答案
高效智能课时作业系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F. 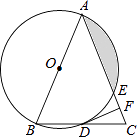
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A( ![]() ,1)在反比例函数y=
,1)在反比例函数y= ![]() 的图象上.
的图象上.
(1)求反比例函数y= ![]() 的表达式;
的表达式;
(2)在x轴的负半轴上存在一点P,使得S△AOP= ![]() S△AOB , 求点P的坐标;
S△AOB , 求点P的坐标;
(3)若将△BOA绕点B按逆时针方向旋转60°得到△BDE.直接写出点E的坐标,并判断点E是否在该反比例函数的图象上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉淇准备完成题目:化简:![]() ,发现系数“
,发现系数“![]() ”印刷不清楚.
”印刷不清楚.
(1)他把“![]() ”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
(2)他妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“![]() ”是几?
”是几?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于有理数a、b,定义运算:a![]() b=a×b-a-b+1.
b=a×b-a-b+1.
(1)计算5![]() (-2)与(-2)
(-2)与(-2)![]() 5的值,并猜想a
5的值,并猜想a![]() b与b
b与b![]() a的大小关系;
a的大小关系;
(2)求(-3)![]() [4
[4![]() (-2)]的值.
(-2)]的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”. 应用:在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点C的极坐标应记为( )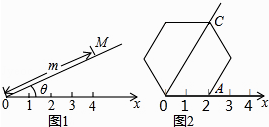
A.(60°,4)
B.(45°,4)
C.(60°,2 ![]() )
)
D.(50°,2 ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现在,苏宁商场进行促销活动,出售一种优惠购物卡(注:此卡只作为购物优惠凭证不能顶替货款),花300元买这种卡后,凭卡可在这家商场按标价的8折购物.
(1)顾客购买多少元金额的商品时,买卡与不买卡花钱相等?在什么情况下购物合算?
(2)小张要买一台标价为3500元的冰箱,如何购买合算?小张能节省多少元钱?
(3)小张按合算的方案,把这台冰箱买下,如果商场还能盈利25%,这台冰箱的进价是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是用大小相等的小正方形按一定规律拼成的,则第10个图形是_________个小正方形,第n 个图形是___________个小正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为4,则BE等于________.
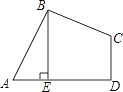
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com