
【题目】在平面直角坐标系中,已知一次函数y=﹣![]() x+6与x,y轴分别交于A,B两点,点C(0,n)是y轴上一点,把坐标平面沿直线AC折叠,点B刚好落在x轴上,则点C的坐标是( )
x+6与x,y轴分别交于A,B两点,点C(0,n)是y轴上一点,把坐标平面沿直线AC折叠,点B刚好落在x轴上,则点C的坐标是( )
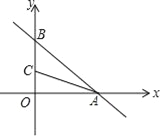
A. (0,3) B. (0,![]() ) C. (0,
) C. (0,![]() ) D. (0,
) D. (0,![]() )
)
【答案】C
【解析】
过C作CD⊥AB于D,先求出A,B的坐标,分别为A(8,0),B(0,6),得到AB的长,再根据折叠的性质得到AC平分∠OAB,得到CD=CO=n,DA=OA=8,则DB=10-8=2,BC=6-n,在Rt△BCD中,利用勾股定理得到n的方程,解方程求出n即可.
过C作CD⊥AB于D,如图,
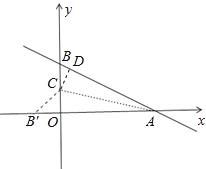
对于直线y=![]() x+6,
x+6,
当x=0,得y=6;当y=0,x=8,
∴A(8,0),B(0,6),即OA=8,OB=6,
∴AB=10,
又∵坐标平面沿直线AC折叠,使点B刚好落在x轴上,
∴AC平分∠OAB,
∴CD=CO=n,则BC=6n,
∴DA=OA=8,
∴DB=108=2,
在Rt△BCD中,DC2+BD2=BC2,
∴n2+22=(6n)2,解得n=![]() ,
,
∴点C的坐标为(0,![]() ).
).
故选:C.


科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是BC的中点,点E是AD上任意一点.
(1)如图1,连接BE、CE,问:BE=CE成立吗?并说明理由;
(2)如图2,若∠BAC=45°,BE的延长线与AC垂直相交于点F时,问:EF=CF成立吗?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某车间有技术工人85人,平均每天每人可加工甲种部件16个或乙种部件10个,2个甲种部件和3个乙种部件配成一套,问加工甲、乙两种部件各安排多少人才能使每天加工的两种部件刚好配套?并求出加工了多少套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上的点A表示的数为6,点B表示的数为﹣4,点C到点A、点B的距离相等,动点P从点B出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为x(x大于0)秒.
(1)点C表示的数是 ;
(2)当x= 秒时,点P到达点A处?
(3)运动过程中点P表示的数是 (用含字母x的式子表示);
(4)当P,C之间的距离为2个单位长度时,求x的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于有理数a、b,定义运算:a![]() b=a×b-a-b+1.
b=a×b-a-b+1.
(1)计算5![]() (-2)与(-2)
(-2)与(-2)![]() 5的值,并猜想a
5的值,并猜想a![]() b与b
b与b![]() a的大小关系;
a的大小关系;
(2)求(-3)![]() [4
[4![]() (-2)]的值.
(-2)]的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC为直角梯形,A(4,0),B(3,4),C(0,4).点M从O出发以每秒2个单位长度的速度向A运动;点N从B同时出发,以每秒1个单位长度的速度向C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP垂直x轴于点P,连接AC交NP于Q,连接MQ.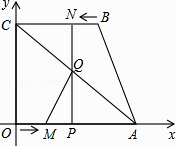
(1)点(填M或N)能到达终点;
(2)求△AQM的面积S与运动时间t的函数关系式,并写出自变量t的取值范围,当t为何值时,S的值最大;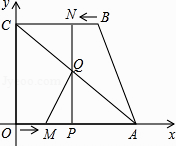
(3)是否存在点M,使得△AQM为直角三角形?若存在,求出点M的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1:y=kx+b平行于直线y=x﹣1,且与直线l2: ![]() 相交于点P(﹣1,0).
相交于点P(﹣1,0).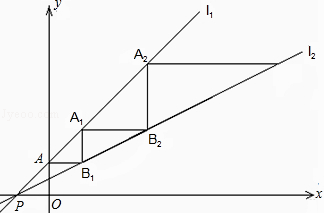
(1)求直线l1、l2的解析式;
(2)直线l1与y轴交于点A.一动点C从点A出发,先沿平行于x轴的方向运动,到达直线l2上的点B1处后,改为垂直于x轴的方向运动,到达直线l1上的点A1处后,再沿平行于x轴的方向运动,到达直线l2上的点B2处后,又改为垂直于x轴的方向运动,到达直线l1上的点A2处后,仍沿平行于x轴的方向运动,…
照此规律运动,动点C依次经过点B1 , A1 , B2 , A2 , B3 , A3 , …,Bn , An , …
①求点B1 , B2 , A1 , A2的坐标;
②请你通过归纳得出点An、Bn的坐标;并求当动点C到达An处时,运动的总路径的长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=ax+b的图象与反比例函数y= ![]() 的图象交于第二、四象限内的A、B两点,与y轴交于C点,过A作AH⊥y轴于H,OH=3,tan∠AOH=
的图象交于第二、四象限内的A、B两点,与y轴交于C点,过A作AH⊥y轴于H,OH=3,tan∠AOH= ![]() ,点B的坐标为(m,﹣2).
,点B的坐标为(m,﹣2). 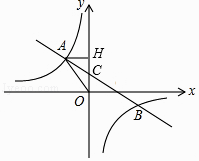
(1)求△AHO的周长;
(2)求反比例函数和一次函数的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com